Tập xác định của 6 mũ x Đầy đủ
Thủ Thuật Hướng dẫn Tập xác lập của 6 mũ x Chi Tiết
Bạn đang tìm kiếm từ khóa Tập xác lập của 6 mũ x được Update vào lúc : 2022-05-04 22:22:09 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.Tập xác lập của biểu thức là toàn bộ những số thực trừ trường hợp biểu thức không xác lập. Trong trường hợp này, không còn số thực nào làm cho biểu thức không xác lập.
Nội dung chính- 1. Tập xác lập của hàm số mũ
- 2. Tập xác lập của hàm lũy thừa
- 3. Tập xác lập của hàm số lôgarit
Ký Hiệu Khoảng:
Ký Hiệu Xây Dựng Tập Hợp:
Skip to content
trang chủ Giáo viên- Học Sinh Bài giảng toán Cách tìm tập xác lập của hàm số mũ, lũy thừa, logarit
Cách tìm tập xác lập của hàm số mũ, lũy thừa, logarit. Tìm tập xác lập của hàm số là một dạng bài điển hình trong những đề thi, kiểm tra và đề thi THPTQG. Bài viết sẽ hỗ trợ những em phân biệt được cách tìm TXĐ của 3 loại hàm số trên.
tập xác lập của hàm số mũ 1. Tập xác lập của hàm số mũ
Cho hàm số $$y = a^xleft( a > 0;a ne 1 right)$$
TXĐ của hàm số là R
Mở rộng hàm số $$y = a^uleft( x right)left( a > 0;a ne 1 right)$$ . Muốn tìm TXĐ của hàm số này, ta chỉ giải Đk để u(x) có nghĩa.
Ví dụ: Tìm TXĐ của hàm số $$y = e^sqrt x^2 + 2x – 3 $$
Giải: Đk $$x^2 + 2x – 3 ge 0 Leftrightarrow left[ matrix x ge 1 hfill cr
x le – 3 hfill cr right.$$
Vậy TXĐ là $$D = left( – infty ; – 3 right] cup left[ 1; + infty right)$$
2. Tập xác lập của hàm lũy thừa
Theo quy ước của sách giáo khoa giải tích 12 thì hàm số lũy thừa có tập xác lập tùy từng lũy thừa. Có toàn bộ 3 trường hợp rất khác nhau về lũy thừa ảnh hưởng đến tập xác lập là: Lũy thừa với số mũ nguyên dương; Lũy thừa số mũ nguyên không dương; Lũy thừa số mũ không nguyên.
Cho hàm lũy thừa $$y = left[ uleft( x right) right]^alpha $$
- $$alpha in ^ + $$ : Tìm đk để u(x) xác lập
- $$alpha in ^ – $$ hoặc $$alpha = 0$$ thì tìm đk để u(x) xác lập và u(x)#0
- $$alpha notin $$ thì tìm đk để u(x) xác lập và u(x) > 0
Chú ý : Hàm số $$y = sqrt x $$ có TXĐ là $$left[ 0; + infty right)$$ trong lúc hàm số $$y = x^1 over 2$$ có TXĐ là $$left( 0; + infty right)$$
Hàm số $$y = root 3 of x $$ có TXĐ là R còn hàm số $$y = x^1 over 3$$ có TXĐ là $$left( 0; + infty right)$$
Nên hàm số $$y = sqrt x $$ khác hàm số $$y = x^1 over 2$$
3. Tập xác lập của hàm số lôgarit
Cho hàm số $$y = log _axleft( a > 0;a ne 1 right)$$
TXĐ là $$left( 0; + infty right)$$
Mở rộng hàm số $$y = log _auleft( x right)left( a > 0;a ne 1 right)$$
thì Đk là thì Đk xác lập là u(x)>0 và u(x) xác lập.
Ví dụ: Tìm tập xác lập của hàm số $$y = log _3left( 2sqrt x – 1 right)$$
Giải: Điều kiện $$left{ matrix 2sqrt x – 1 hfill cr x ge 0 hfill cr right. Leftrightarrow left{ matrix sqrt x > 1 over 2 hfill cr
x ge 0 hfill cr right. Leftrightarrow x > 1 over 4$$
Vậy TXĐ $$D = left( 1 over 4; + infty right)$$
Bài viết cùng series:Like share và ủng hộ chúng mình nhé:
Nếu thấy bài biết hay và hữu ích hãy donate cho blog nhé
Donate qua ví MOMO:
Donate qua Viettel Pay:
Cách xác lập tập xác lập của hàm số mũ – Logarit không hề khó bởi đây đều là những kiến thức và kỹ năng cơ bản từ sách giáo khoa . Nếu toàn bộ chúng ta không thuộc được công thức tính hay tìm ra một phương pháp nhanh nhất có thể để tính thì chắc như đinh đó là cả 1 yếu tố với bạn . Đối với tìm tập xác lập của hàm số mũ và hàm Logarit thì toàn bộ chúng ta hoàn toàn hoàn toàn có thể vận dụng theo những hướng dẫn dưới đây từ Legoland nhé .
Có thể bạn quan tâm :
y = ax
Trong số đó : a > 0 và a ≠ 1
Và tập xác lập của hàm số mũ này đó đó là R .
Chú ý : Chúng ta nên nhớ đó là lúc toàn bộ chúng ta gặp bài toán tìm tập xác lập của hàm số
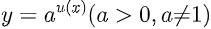
Thì toàn bộ chúng ta chỉ việc viết Đk khiến cho u(x) xác lập.
5 ví dụ về tính chất tập xác lập của hàm số mũ :
Ví dụ 1 : Tìm tập xác lập của hàm số mũ :
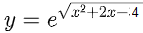
Lời giải :
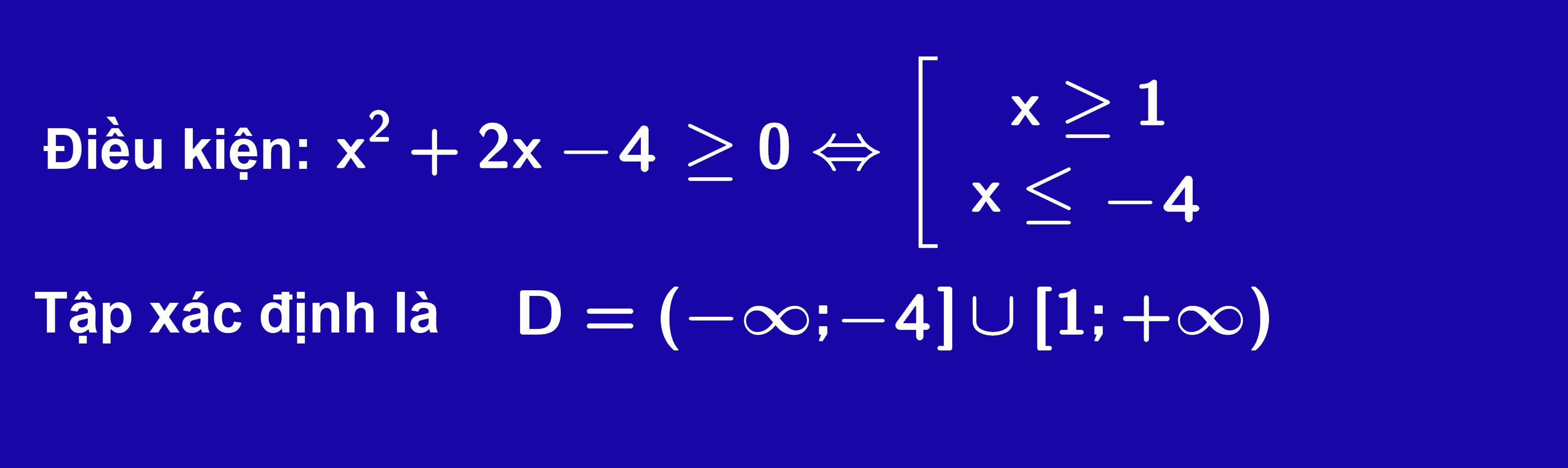
Ví dụ 2 : Tìm tập xác lập D của hàm số
y=(x2-1)-8
Lời giải :
Hàm số xác lập khi và chỉ khi x2-1 ≠ 0 . Suy ra tập xác lập của hàm số Y là x ≠ ±1
Ví dụ 3 : Tìm tập xác lập của hàm số Y
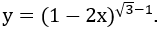
Lời giải :
Để tìm kiếm được tập xác lập thì toàn bộ chúng ta phải là một hàm có nghĩa trước . Chính vì thế để hàm có nghĩa thì 1-2x > 0 => x < 1/2
Vậy tập xác lập của hàm số Y là : x < 1/2
Ví dụ 4 : Tìm tập xác lập của hàm số Y
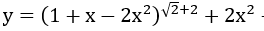
Lời giải :
Hàm số xác định khi và chỉ khi : 1+x-2x2 > 0 . Từ đó ta sua ra tập xác lập của hàm số Y là : -1/2 < x < 1
Ví dụ 5 : Tìm tập xác lập của hàm số Y :
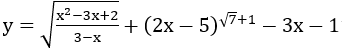
Lời giải :
Trong bài này để hàm số có nghĩa thì toàn bộ chúng ta xét 2 trường hợp :
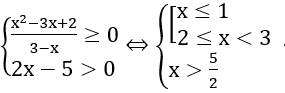
Và toàn bộ chúng ta hoàn toàn có thể suy ra tập xác lập D là : 5/2 < x < 3 hoặc D 5/2; 3
Ta có công thức chung của hàm số logarit :
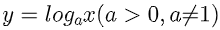
Để xác lập được tập xác lập của hàm logarit Y thì toàn bộ chúng ta phải có Đk : a >0 và a # 1 . Vậy hàm số logarit sẽ có được tập xác lập là : (0;+∞).
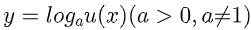
Điều kiện để hàm logorit xác lập đí là u(x) > 0 và u(x) phải được xác lập .
Các ví vụ về phương pháp tính tập xác lập của hàm logarit
Ví dụ 1 : Tìm tập xác lập D của hàm số Y :
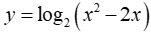
Lời giải :
Hàm số xác lập khi x2 – 2x > 0 ⇔ x < 0 ∪ x > 2
Vậy tập xác lập của hàm số logarit sẽ là D = (-∞ 0) ∪ (2; +∞)
Ví dụ 2 : Tìm tập xác lập của hàm số Logarit Y
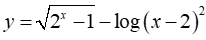
Lời giải :
Để xác lập được tập xác lập thì hàm phải đủ Đk sau :
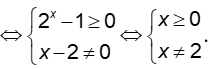
Từ đó suy ra tập xác lập của hàm số Logarit D = ([0; +∞]2)
Ví dụ 3 : Tìm toàn bộ những giá trị thực của tham số m để hàm số :
Y = log(x2-2x-m+1)
hàm có tập xác lập là R.
Lời giải :Để hàm số y=log(x2-2x-m+1) có tập xác lập là R thì toàn bộ chúng ta phải có những Đk như sau :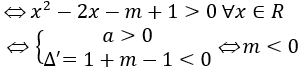
Từ đó suy ra tập xác lập của hàm số logarit là : mọi X thuộc R và m < 0Ví dụ 4 : Tìm tập xác lập của hàm số logarit Y :
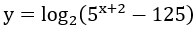
Lời giải :
Để hàm số xác định có nghĩa khi : 5x+2-125 > 0 ⇔ 5x+2 > 53 ⇔ x > 1.
Vậy tập xác lập D=(1;+∞).
Ví dụ 5 : Tìm tập xác lập của hàm số logarit Y :
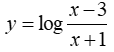
Lời giải :
Hàm số chỉ xác lập khi :
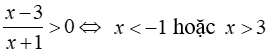
Vậy tập xác lập của hàm số là : D =(x<-1 hoặc x>3)
Với công thức và cách xác lập tập xác lập của hàm số mũ và tập xác lập của hàm số logarit kèm theo những ví dụ từ Bất động sản Legoland kỳ vọng mọi người hoàn toàn có thể vận dụng được thực tiễn vào bài học kinh nghiệm tay nghề tốt nhất .
Reply
4
0
Chia sẻ
Share Link Cập nhật Tập xác lập của 6 mũ x miễn phí
Bạn vừa đọc nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Review Tập xác lập của 6 mũ x tiên tiến và phát triển nhất và ShareLink Download Tập xác lập của 6 mũ x Free.