Cho đường thẳng có hệ số góc k 2 tìm một vectơ pháp tuyến của đường thẳng 2022
Kinh Nghiệm về Cho đường thẳng có thông số góc k 2 tìm một vectơ pháp tuyến của đường thẳng Chi Tiết
Quý khách đang tìm kiếm từ khóa Cho đường thẳng có thông số góc k 2 tìm một vectơ pháp tuyến của đường thẳng được Cập Nhật vào lúc : 2022-05-01 18:58:13 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Đường thẳng trải qua điểm D(4;1) và có thông số góc k = -2 có phương trình tham số là:
A. x = - 2 + 4 t y = 1 + t
B. x = 4 + t y = 1 - 2 t
C. x = 4 + t y = 1 + 2 t
D. x = 1 + 2 t y = 4 + t
Các vướng mắc tương tự
Phương trình tham số của đường thẳng ∆ trải qua điểm M(2; 3) và có thông số góc k = 4 là:
A.y = 4(x – 2) + 3
B. 4x – y – 5 = 0
C. x = 2 + t y = 3 + 4 t , t ∈ R
D. x = 2 + 2 t y = 3 + t , t ∈ R
Cho đường thẳng d có phương trình tham số x = 2 - 3 t y = - 1 + 2 t ( t ∈ ℝ ) và điểm A(3,5 ; -2). Điểm A thuộc d ứng với giá trị nào của t ?
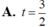
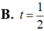
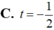
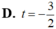
và cắt đường thẳng d 2 : x = -1, y = t, z = 1 + t
A. d : x - 1 = y - 1 1 = z - 1 2
B. d : x - 1 = y + 1 1 = z + 1 2
C. d : x = - t ; y = t ; z = 1 + 2 t
D. d : x 3 = y - 1 1 = z - 1 1
Đường thẳng d trải qua điểm M(2;-3) và vuông góc với đường thẳng d ' : x = 2 - t y = 3 - 2 t , t ∈ ℝ có phương trình:
A. x + 2y + 4 = 0
B. 2x + 3y + 4 = 0
C. 2x - 3y + 1 = 0
D. x - 2y - 4 = 0
Bài 1: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng Δ, với:a, d: 2x-y+1=0, Δ: 3x-4y+2=0b, d: x-2y+4=0, Δ: 2x+y-2=0c, d: x+y-1=0, Δ: x-3y+3=0 d, d: 2x-3y+1=0, Δ: 2x-3y-1=0 Bài 2: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua điểm I với:a, d: 2x-y+1=0, I(2;1)b, d: x-2y+4=0, I(-3;0)c, d: x+y-1=0, I(0:3)
d, d: 2x-3y+1=0, I trùng O(0;0)
GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
Vectơ chỉ phương của đường thẳng là gì? Vectơ chỉ phương trong oxyz như nào? Cách tìm Vectơ chỉ phương của đường thẳng ra sao? … Đây là một trong những phần kiến thức và kỹ năng Toán 10 vô cùng quan trong được nhiều học viên quan tâm. Bài viết ngày hôm nay, THPT Sóc Trăng sẽ giải đáp tường tận cho những bạn nhé !
I. LÝ THUYẾT VỀ VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG
1. Vecto chỉ phương của đường thẳng là gì?
Bạn đang xem: Vectơ chỉ phương là gì? Cách tìm Vectơ chỉ phương của đường thẳng cực hay
– Giá của vectơ là đường thẳng trải qua điểm gốc và điểm ngọn của vectơ đó.
– Cho đường thẳng d. Ta có vecto
được gọi là vectơ chỉ phương (VTCP) của đường thẳng d nếu giá của nó tuy nhiên tuy nhiên hoặc trùng với d.
– Nếu
là VTCP của d thì 
cũng là VTCP của d.
– VTCP và VTPT vuông góc với nhau
. Đây đó đó là cách chuyển từ VTCP sang VTPT và ngược lại.
– Ta hoàn toàn có thể thuận tiện và đơn thuần và giản dị xác lập được đường thẳng lúc biết một điểm thuộc đường thẳng và VTCP của đường thẳng đó.
2. Hệ số góc của đường thẳng
– Phương trình đường thẳng d có dang: y = kx + b hay kx – y – b = 0
+ Hệ số góc của đường thẳng là k.
+ Vectơ pháp tuyến của đường thẳng là
+ Vectơ chỉ phương của đường thẳng là:
Ví dụ: Cho phương trình đường thẳng 3x + 2y = 1. Xác định vectơ chỉ phương, vectơ pháp tuyến, thông số góc của đường thẳng.
Hướng dẫn:
+ Vectơ chỉ pháp tuyến của đường thẳng là
+ Vectơ chỉ phương của đường thẳng là:
+Ta viết lại phương trình đường thẳng
. Hệ số góc của đường thẳng là 
.
3. Phương trình tham số của đường thẳng
– Đường thẳng d trải qua A(m, n) nhận
làm vectơ chỉ phương có phương trình tham số là:
Ví dụ 1 : Lập phương trình tham số trải qua điểm A(1, 2) và vectơ chỉ phương
.
Hướng dẫn giải
Phương trình tham số của đường thẳng
Ví dụ 2: Vectơ chỉ phương của đường thẳng d: 2x – 5y – 100 = 0 là:
A.
= (2; -5)
B. = (2; 5)
C. = (5; 2)
D. =( -5; 2)
Hướng dẫn giải
Đường thẳng d có VTPT là
( 2 ;- 5) .
⇒ Đường thẳng có VTCP là
( 5 ; 2).
4. Ứng dụng trong mặt phẳng tọa độ
Những bài toán ứng dụng tính chất của vectơ chỉ phương thường gặp nhất:
+ Xác định vectơ chỉ phương cho trước.
+ Viết phương trình đường thẳng trải qua một điểm và VTCP cho trước.
+ Xác xác định trí tương đối của 2 đường thẳng.
+ Tính khoảng chừng cách từ một điểm đến một đường thẳng.
+ Biện luận, chứng tỏ phương trình đường thẳng.
Các tính chất của vecto chỉ phương sẽ xuất hiện xuyên thấu trong những bài tập tổng hợp về phương trình đường thẳng, học viên cần nắm vững nội dung định nghĩa, tính chất của vectơ pháp tuyến.
II. CÁCH TÌM VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG CỰC HAY
1. Phương pháp giải
+ Cho đường thẳng d, một vecto u→ được gọi là VTCP của đường thẳng d nếu u→ có mức giá tuy nhiên tuy nhiên hoặc trùng với đường thẳng d.
+ Nếu vecto u→( a; b) là VTCP của đường thẳng d thì vecto k.u→ ( với k ≠ 0) cũng là VTCP của đường thẳng d.
+ Nếu đường thẳng d có VTPT n→( a; b) thì đường thẳng d nhận vecto n→( b; -a) và n’→( – b;a) làm VTPT.
2. Ví dụ minh họa
Ví dụ 1: Cho đường thẳng d trải qua A(- 2; 3) và điểm B(2; m + 1) . Tìm m để đường thẳng d nhận u→( 2; 4) làm VTCP?
A. m = – 2 B. m = -8 C. m = 5 D. m = 10
Lời giải
Đường thẳng d trải qua hai điểm A và B nên đường thẳng d nhận vecto AB→( 4; m – 2) làm VTCP.
Lại có vecto u→(2; 4) làm VTCP của đường thẳng d. Suy ra hai vecto u→ và ab→ cùng phương nên tồn tại số k sao cho: u→ = kAB→
Vậy m = 10 là giá trị cần tìm .
Chọn D.
Ví dụ 2. Vectơ nào dưới đấy là một vectơ chỉ phương của đường thẳng trải qua hai điểm A( a; 0) và B( 0; b)
A. u→( -a; b) B. u→( a; b) C. u→( a + b; 0) D. u→( – a; – b)
Lời giải
Đường thẳng AB trải qua điểm A và B nên đường thẳng này nhận AB→(-a;b) làm vecto chỉ phương.
Chọn A.
Ví dụ 3. Đường thẳng d có một vectơ pháp tuyến là u→ = (-2; -5) . Đường thẳng ∆ vuông góc với d có một vectơ chỉ phương là:
A. u1→ = (5; -2) B. u2→ = (-5; 2) C. u3→ = (2; 5) D. u4→ = (2; -5)
Lời giải
Khi hai tuyến phố thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia nên :
Lại có hai vecto u∆→( -2; -5) và u→( 2;5) cùng phương nên đường thẳng ∆ nhận vecto u→( 2; 5) làm VTCP.
Chọn C.
Ví dụ 4. Đường thẳng d có một vectơ chỉ phương là u→ = (3; -4). Đường thẳng ∆ tuy nhiên tuy nhiên với d có một vectơ pháp tuyến là:
A. n1→ = (4; 3) B. n2→ = (- 4; 3) C. n3→ = (3; 4) D. n4→ = (3; – 4)
Lời giải
Khi hai tuyến phố thẳng tuy nhiên tuy nhiên với nhau thì VTCP ( VTPT) của đường thẳng này cũng là VTCP (VTPT) của đường thẳng kia nên:
→ u∆→ = ud→ = (3; -4) → n∆→ = (4; 3)
Chọn A
III. BÀI TẬP VẬN DỤNG
1. Bài tập có đáp án
Bài 1: Vectơ chỉ phương của đường thẳng d
là:
A. u1→ = (2; -3) B. u2→ = (3; -1) C. u3→ = (3; 1) D. u4→ = (3; -3)
Lời giải
Một VTCP của đường thẳng d là u→( 3; -1)
Chọn B
Bài 2: Vectơ nào dưới đấy là một vectơ chỉ phương của đường thẳng trải qua hai điểm A(-3; 2) và B( 1; 4) ?
A. u1→ = (-1; 2) B. u2→ = (2; 1) C. u3→ = (- 2; 6) D. u4→ = (1; 1)
Lời giải
+ Đường thẳng AB trải qua hai điểm A và B nên đường thẳng này nhận vecto AB→( 4; 2) làm vecto chỉ phương .
+ Lại có vecto AB→ và u→( 2;1) là hai vecto cùng phương nên đường thẳng AB nhận vecto u→( 2;1) là VTCP.
Chọn B.
Bài 3: Vectơ chỉ phương của đường thẳng
= 1 là:
A. u4→ = (-2; 3) B. u2→ = (3; -2) C. u3→ = (3; 2) D. u1→ = (2; 3)
Hướng dẫn giải:
Ta đưa phương trình đường thẳng đã cho về dạng tổng quát:
= 1 ⇔ 2x + 3y – 6 = 0 nên đường thẳng có VTPT là n→ = (2; 3)
Suy ra VTCP là u→ = (3; – 2) .
Chọn B.
Bài 4: Vectơ chỉ phương của đường thẳng d: 2x – 5y – 100 = 0 là :
A. u→ = (2; -5) B. u→ = (2; 5) C. u→ = (5; 2) D. u→=( -5; 2)
Lời giải
Đường thẳng d có VTPT là n→( 2 ;- 5) .
⇒ đường thẳng có VTCP là u→( 5 ; 2).
Chọn C.
2. Bài rèn luyện thêm:
Câu 1. Vectơ chỉ phương của đường thẳng d x = 2+3t và y = -3-t là:
A.
= (2; -3)
B.
= (3; -1)
C.
= (3; 1)
D.
= (3; -3)
Câu 2: Vectơ nào dưới đấy là một vectơ chỉ phương của đường thẳng trải qua hai điểm A(-3; 2) và B (1; 4)?
A.
= (-1; 2)
B.
= (2; 1)
C.
= (- 2; 6)
D.
= (1; 1)
Câu 3: Vectơ chỉ phương của đường thẳng x = 2+3t và y = -3-t = 1 là:
A.
= (-2; 3)
B.
= (3; -2)
C.
= (3; 2)
D.
= (2; 3)
Câu 4: Vectơ chỉ phương của đường thẳng d: 2x – 5y – 100 = 0 là:
A.
= (2; -5)
B.
= (2; 5)
C.
= (5; 2)
D.
=( -5; 2)
Câu 5: Vectơ nào dưới đấy là một vectơ pháp tuyến của đường thẳng trải qua hai điểm A(2 ; 3) và B( 4 ;1)
A.
= (2; -2)
B.
= (2; -1)
C.
= (1; 1)
D.
= (1; -2)
Câu 6: Vectơ nào dưới đấy là một vectơ chỉ phương của đường thẳng tuy nhiên tuy nhiên với trục Ox
A.
= (1; 0).
B.
= (0; -1)
C.
= (1; 1)
D.
= (1; – 1)
Câu 7: Cho đường thẳng d trải qua A( 1; 2) và điểm B(2; m). Tìm m để đường thẳng d nhận
(1; 3) làm VTCP?
A. m = – 2
B. m = -1
C. m = 5
D. m = 2
Câu 8: Cho đường thẳng d trải qua A(- 2; 3) và điểm B(2; m + 1) . Tìm m để đường thẳng d nhận
( 2; 4) làm VTCP?
A. m = – 2
B. m = -8
C. m = 5
D. m = 10
Câu 9: Vectơ nào dưới đấy là một vectơ chỉ phương của đường thẳng trải qua hai điểm A( a; 0) và B( 0; b)
A.
( -a; b)
B.
( a; b)
C.
( a + b; 0)
D.
( – a; – b)
Trên đây THPT Sóc Trăng đã trình làng đến những bạn lý thuyết về Vectơ chỉ phương và cách tìm Vectơ chỉ phương của đường thẳng cực hay. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu giúp những bạn dạy và học tốt hơn. Xem thêm chuyên đề tích vô vị trí hướng của hai vectơ tại đường link này bạn nhé !
Đăng bởi: THPT Sóc Trăng
Chuyên mục: Giáo dục đào tạo và giảng dạy
Reply
3
0
Chia sẻ
Chia Sẻ Link Cập nhật Cho đường thẳng có thông số góc k 2 tìm một vectơ pháp tuyến của đường thẳng miễn phí
Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Clip Cho đường thẳng có thông số góc k 2 tìm một vectơ pháp tuyến của đường thẳng tiên tiến và phát triển nhất và Chia SẻLink Download Cho đường thẳng có thông số góc k 2 tìm một vectơ pháp tuyến của đường thẳng Free.