Phân tích đa thức thành nhân tử: x 3 y 3 2x 2 2xy 2022
Mẹo Hướng dẫn Phân tích đa thức thành nhân tử: x 3 y 3 2x 2 2xy Mới Nhất
You đang tìm kiếm từ khóa Phân tích đa thức thành nhân tử: x 3 y 3 2x 2 2xy được Cập Nhật vào lúc : 2022-04-14 16:25:02 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Sách giải toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng phương pháp phối hợp nhiều phương pháp giúp bạn giải những bài tập trong sách giáo khoa toán, học tốt toán 8 sẽ hỗ trợ bạn rèn luyện kĩ năng suy luận hợp lý và hợp logic, hình thành kĩ năng vận dụng kết thức toán học vào đời sống và vào những môn học khác:
Lời giải
2x3y – 2xy3 – 4xy2 – 2xy
= 2xy(x2 – y2 – 2y – 1)
= 2xy[x2 – (y2 + 2y + 1)]
= 2xy[x2 – (y + 1)2 ]
= 2xy(x + y + 1)(x – y – 1)
a) Tính nhanh x2 + 2x + 1 – y2 tại x = 94,5 và y = 4,5.
b) Khi phân tích đa thức x2 + 4x – 2xy – 4y + y2 thành nhân tử, bạn Việt làm như sau:
x2 + 4x – 2xy – 4y + y2 = (x2 – 2xy + y2) + (4x – 4y)
= (x – y)2 + 4(x – y)
= (x – y)(x – y + 4).
Em hãy chỉ rõ trong cách làm trên, bạn Việt đã sử dụng những phương pháp nào để phân tích đa thức thành nhân tử.
Lời giải
a) x2 + 2x + 1 – y2 = (x + 1)2-y2 = (x + y + 1)(x – y + 1)
Thay x = 94,5 và y = 4,5 ta có:
(x + y + 1)(x – y + 1)
= (94,5 + 4,5 + 1)(94,5 – 4,5 + 1)
= 100.91
= 9100
b) x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x – y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung
a) x3 – 2x2 + x.
b) 2x2 + 4x + 2 – 2y2
c) 2xy – x2 – y2 + 16
Lời giải:
a) x3 – 2x2 + x
= x.x2 – x.2x + x (Xuất hiện nhân tử chung là x)
= x(x2 – 2x + 1) (Xuất hiện hằng đẳng thức (2))
= x(x – 1)2
b) 2x2 + 4x + 2 – 2y2 (có nhân tử chung là 2)
= 2.(x2 + 2x + 1 – y2) (Xuất hiện x2 + 2x + 1 là hằng đẳng thức)
= 2[(x2 + 2x + 1) – y2]
= 2[(x + 1)2 – y2] (Xuất hiện hằng đẳng thức (3))
= 2(x + 1 – y)(x + 1 + y)
c) 2xy – x2 – y2 + 16 (Có 2xy ; x2 ; y2, ta liên tưởng đến HĐT (1) hoặc (2))
= 16 – (x2 – 2xy + y2)
= 42 – (x – y)2 (xuất hiện hằng đẳng thức (3))
= [4 – (x – y)][4 + (x + y)]
= (4 – x + y)(4 + x – y).
Các bài giải Toán 8 Bài 9 khác
Chứng minh rằng (5n + 2)2 – 4 chia hết cho 5 với mọi số nguyên n.
Lời giải:
Ta có:
(5n + 2)2 – 4
= (5n + 2)2 – 22
= (5n + 2 – 2)(5n + 2 + 2)
= 5n(5n + 4)
Vì 5 ⋮ 5 nên 5n(5n + 4) ⋮ 5 ∀n ∈ Ζ.
Vậy (5n + 2)2 – 4 luôn chia hết cho 5 với n ∈ Ζ
Các bài giải Toán 8 Bài 9 khác
a) x2 – 3x + 2
b) x2 + x – 6
c) x2 + 5x + 6
(Gợi ý : Ta không thể vận dụng ngay những phương pháp đã học để phân tích nhưng nếu tách hạng tử – 3x = – x – 2x thì ta có x2 – 3x + 2 = x2 – x – 2x + 2 và từ đó thuận tiện và đơn thuần và giản dị phân tích tiếp.
Cũng hoàn toàn có thể tách 2 = – 4 + 6, khi đó ta có x2 – 3x + 2 = x2 – 4 – 3x + 6, từ đó thuận tiện và đơn thuần và giản dị phân tích tiếp)
Lời giải:
Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.
x2 – 3x + 2
= x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2)
= x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2
= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6
= (x2 – 22) – 3(x – 2)
= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)
b) x2 + x – 6
= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c) x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)
a) x2 – 3x + 2
(Vì có x2 và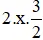 
nên ta thêm bớt 
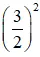để xuất hiện HĐT)
= (x – 2)(x – 1)
b) x2 + x – 6
= (x – 2)(x + 3).
c) x2 + 5x + 6
= (x + 2)(x + 3).
Các bài giải Toán 8 Bài 9 khác
a) x3 + 2x2y + xy2 – 9x
b) 2x – 2y – x2 + 2xy – y2
c) x4 – 2x2
Lời giải:
a) x3 + 2x2y + xy2 – 9x
(Có x là nhân tử chung)
= x(x2 + 2xy + y2 – 9)
(Có x2 + 2xy + y2 là hằng đẳng thức)
= x[(x2 + 2xy + y2) – 9]
= x[(x + y)2 – 32]
(Xuất hiện hằng đẳng thức (3)]
= x(x + y – 3)(x + y + 3)
b) 2x – 2y – x2 + 2xy – y2
(Có x2 ; 2xy ; y2 ta liên tưởng đến HĐT (1) hoặc (2))
= (2x – 2y) – (x2 – 2xy + y2)
= 2(x – y) – (x – y)2
(Có x – y là nhân tử chung)
= (x – y)[2 – (x – y)]
= (x – y)(2 – x + y)
c) x4 – 2x2
(Có x2 là nhân tử chung)
= x2(x2 – 2)
Các bài giải Toán 8 Bài 9 khác
Lời giải:
b) Có: (2x – 1)2 – (x + 3)2 (xuất hiện HĐT (3))
= [(2x – 1) – (x + 3)][(2x – 1) + (x + 3)]
= (2x – 1 – x – 3).(2x – 1 + x + 3)
= (x – 4)(3x + 2)
Vậy (2x – 1)2 – (x + 3)2 = 0
⇔ (x – 4)(3x + 2) = 0
⇔ x – 4 = 0 hoặc 3x + 2 = 0
⇔ x = 4 hoặc x = –2/3
Vậy x = 4 hoặc x = –2/3.
c) Có: x2(x – 3) + 12 – 4x
= x2(x – 3) – 4.(x – 3) (Có nhân tử chung là x – 3)
= (x2 – 4)(x – 3)
= (x2 – 22).(x – 3) (Xuất hiện HĐT (3))
= (x – 2)(x + 2)(x – 3)
Vậy x2(x – 3) + 12 – 4x = 0
⇔ (x – 2)(x + 2)(x – 3) = 0
⇔ x – 2 = 0 hoặc x + 2 = 0 hoặc x – 3 = 0
⇔ x = 2 hoặc x = –2 hoặc x = 3.
Vậy x = 2 hoặc x = –2 hoặc x = 3.
Các bài giải Toán 8 Bài 9 khác
Lời giải:
a) Ta có:
Do đó tại x = 49,75, giá trị biểu thức bằng
b) Ta có:
x2 – y2 – 2y – 1 (Thấy có y2 ; 2y ; 1 ta liên tưởng đến HĐT (1) hoặc (2))
= x2 – (y2 + 2y + 1)
= x2 – (y + 1)2 (Xuất hiện HĐT (3))
= (x – y – 1)(x + y + 1)
Với x = 93, y = 6 thì:
(93 – 6 – 1)(93 + 6 + 1) = 86.100 = 8600
Các bài giải Toán 8 Bài 9 khác
a) x2 – 4x + 3 ; b) x2 + 5x + 4
c) x2 – x – 6 ; d) x4 + 4
(Gợi ý câu d): Thêm và bớt 4x2 vào đa thức đã cho)
Lời giải:
a) Cách 1: x2 – 4x + 3
= x2 – x – 3x + 3
(Tách –4x = –x – 3x)
= x(x – 1) – 3(x – 1)
(Có x – 1 là nhân tử chung)
= (x – 1)(x – 3)
Cách 2: x2 – 4x + 3
= x2 – 2.x.2 + 22 + 3 – 22
(Thêm bớt 22 để sở hữu HĐT (2))
= (x – 2)2 – 1
(Xuất hiện HĐT (3))
= (x – 2 – 1)(x – 2 + 1)
= (x – 3)(x – 1)
b) x2 + 5x + 4
= x2 + x + 4x + 4
(Tách 5x = x + 4x)
= x(x + 1) + 4(x + 1)
(có x + 1 là nhân tử chung)
= (x + 1)(x + 4)
c) x2 – x – 6
= x2 + 2x – 3x – 6
(Tách –x = 2x – 3x)
= x(x + 2) – 3(x + 2)
(có x + 2 là nhân tử chung)
= (x – 3)(x + 2)
d) x4 + 4
= (x2)2 + 22
= x4 + 2.x2.2 + 4 – 4x2
(Thêm bớt 2.x2.2 để sở hữu HĐT (1))
= (x2 + 2)2 – (2x)2
(Xuất hiện HĐT (3))
= (x2 + 2 – 2x)(x2 + 2 + 2x)
Các bài giải Toán 8 Bài 9 khác
Lời giải:
A = n3 – n (có nhân tử chung n)
= n(n2 – 1) (Xuất hiện HĐT (3))
= n(n – 1)(n + 1)
n – 1; n và n + 1 là ba số tự nhiên liên tục nên
+ Trong số đó có tối thiểu một số trong những chẵn ⇒ (n – 1).n.(n + 1) ⋮ 2
+ Trong số đó có tối thiểu một số trong những chia hết cho 3 ⇒ (n – 1).n.(n + 1) ⋮ 3
Vậy A ⋮ 2 và A ⋮ 3 nên A ⋮ 6.
Các bài giải Toán 8 Bài 9 khác
Chia Sẻ Link Download Phân tích đa thức thành nhân tử: x 3 y 3 2x 2 2xy miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Clip Phân tích đa thức thành nhân tử: x 3 y 3 2x 2 2xy tiên tiến và phát triển nhất và Chia SẻLink Tải Phân tích đa thức thành nhân tử: x 3 y 3 2x 2 2xy Free.