Cho tứ giác ABCD gọi MN lần lượt là trung điểm của BC và AD Chứng minh vecto BC vecto cả 2 vecto MN Chi tiết
Thủ Thuật Hướng dẫn Cho tứ giác ABCD gọi MN lần lượt là trung điểm của BC và AD Chứng minh vecto BC vecto cả hai vecto MN Chi Tiết
You đang tìm kiếm từ khóa Cho tứ giác ABCD gọi MN lần lượt là trung điểm của BC và AD Chứng minh vecto BC vecto cả hai vecto MN được Update vào lúc : 2022-04-16 10:01:09 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.Xem toàn bộ tài liệu Lớp 10: tại đây
- Giải Toán Lớp 10
- Sách Giáo Viên Đại Số Lớp 10
- Sách giáo khoa đại số 10
- Sách giáo khoa hình học 10
- Sách Giáo Viên Hình Học Lớp 10
- Sách giáo khoa đại số 10 nâng cao
- Sách Giáo Viên Đại Số Lớp 10 Nâng Cao
- Giải Toán Lớp 10 Nâng Cao
- Sách giáo khoa hình học 10 nâng cao
- Sách Giáo Viên Hình Học Lớp 10 Nâng Cao
- Sách Bài Tập Đại Số Lớp 10
- Sách Bài Tập Hình Học Lớp 10
- Sách Bài Tập Đại Số Lớp 10 Nâng Cao
- Sách Bài Tập Hình Học Lớp 10 Nâng Cao
Sách Giải Sách Bài Tập Toán 10 Bài 1: Các định nghĩa giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 10 sẽ hỗ trợ bạn rèn luyện kĩ năng suy luận hợp lý và hợp logic, hình thành kĩ năng vận dụng kết thức toán học vào đời sống và vào những môn học khác:
Bài 1.1 trang 10 Sách bài tập Hình học 10: Hãy tính số những vectơ (khác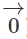 
)mà những điểm đầu và điểm cuối được lấy từ những điểm phân biệt đã cho trong những trường hợp sau:
a) Hai điểm
b) Ba điểm;
c) Bốn điểm.
Lời giải:
a) Với hai điểm A, B có hai vec tơ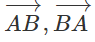 
b) Với ba điểm A, B, C có 6 vec tơ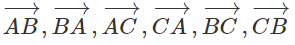 
c) Với bốn điểm A, B, C, D có 12 véctơ. Học sinh tự liệt kê theo quy tắc: hai điểm tạo thành 2 vectơ đối nhau.
Bài 1.2 trang 10 Sách bài tập Hình học 10: Cho hình vuông vắn ABCD có tâm O. Liệt kê toàn bộ những vec tơ bằng nhau (khác vectơ 0) nhận đỉnh và tâm của hình vuông vắn làm điểm đầu và điểm cuối.
Lời giải:
Bài 1.3 trang 10 Sách bài tập Hình học 10: Cho tứ giác ABCD. Gọi M, N, P và Q. lần lượt là trung điểm của những cạnh AB, BC, CD và DA. Chứng minh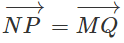 
và
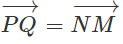
Lời giải:
(h. 1.35)
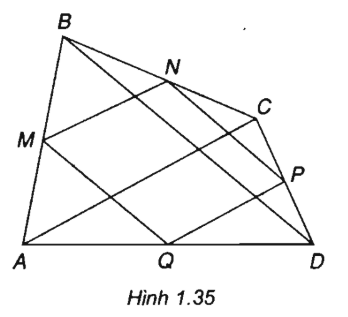
MN = PQ và MN // PQ
Vì chúng đều bằng 0,5AC và đều tuy nhiên tuy nhiên với AC .
Vậy tứ giác MNPQ là hình bình hành nên ta có:
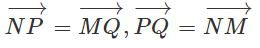
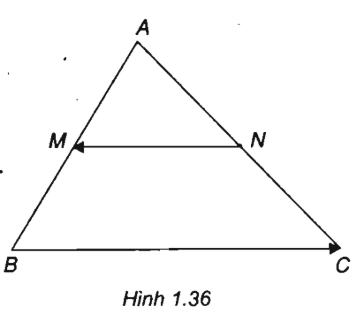
Bài 1.4 trang 10 Sách bài tập Hình học 10: Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm của những cạnh AB và AC. So sánh độ dài của hai vec tơ
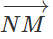và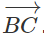 
. Vì sao hoàn toàn có thể nói rằng hai vec tơ này cùng phương?
Lời giải:
(h. 1. 36)
MN // BC và MN = 1/2 BC hay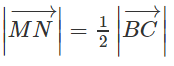 
Vì MN // BC nên
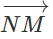và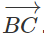 
cùng phương.
Bài 1.5 trang 10 Sách bài tập Hình học 10: Cho tứ giác ABCD, chứng tỏ rằng nếu AB→ = CD→ thì AD→ = BC→
Lời giải:
Tứ giác ABCD có AB→ = CD→ nên AB = DC và AB // CD. Do đó ABCD là hình bình hành, suy ra: AD→ = BC→.
Bài 1.6 trang 10 Sách bài tập Hình học 10: Xác xác định trí tương đối của ba điểm phân biệt A, B và C trong những trường hợp sau:
a)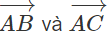 
cùng hướng,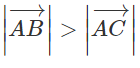 
b)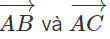 
ngược hướng;
c) 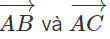cùng phương.
Lời giải:
a) Nếu 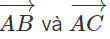cùng hướng, 
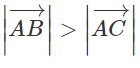thì điểm C nằm trong tâm hai điểm A và B (h.1.38)
b) Nếu 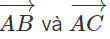ngược hướng thì điểm A nằm trong tâm hai điểm B và C (h. 1.39)
c) Nếu 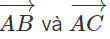cùng phương thì chúng hoàn toàn có thể cùng hướng hoặc ngược hướng.
Trường hợp 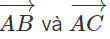cùng hướng
– Nếu 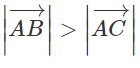thì C nằm trong tâm A và B.
– Nếu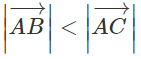 
thì B nằm trong tâm A và C.
Trường hợp Trường hợp 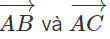ngược hướng thì A nằm trong tâm B và C.
Bài 1.7 trang 10 Sách bài tập Hình học 10: Cho hình bình hành ABCD. Dựng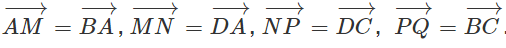 
. Chứng minh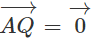 
Lời giải:
(h.1.40)
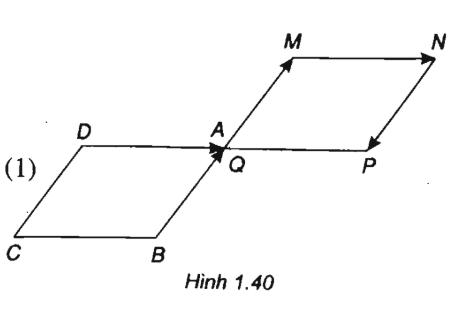
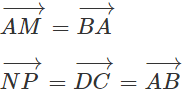
Suy ra AM = NP và AM // NP. Vậy tứ giác AMNP là hình bình hành. (1)
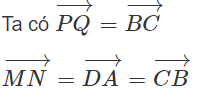
Suy ra PQ = MN và P Q. // MN . Vậy tứ giác MNPQ là hình bình hành (2).
Từ (1) và (2) suy ra A = Q. hay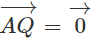 
Chia Sẻ Link Download Cho tứ giác ABCD gọi MN lần lượt là trung điểm của BC và AD Chứng minh vecto BC vecto cả hai vecto MN miễn phí
Bạn vừa tìm hiểu thêm Post Với Một số hướng dẫn một cách rõ ràng hơn về Video Cho tứ giác ABCD gọi MN lần lượt là trung điểm của BC và AD Chứng minh vecto BC vecto cả hai vecto MN tiên tiến và phát triển nhất và ShareLink Tải Cho tứ giác ABCD gọi MN lần lượt là trung điểm của BC và AD Chứng minh vecto BC vecto cả hai vecto MN Free.