Cho hình chóp sabc có đáy ABC là tam giác vuông tại đỉnh A cạnh BC 3a Đầy đủ
Thủ Thuật Hướng dẫn Cho hình chóp sabc có đáy ABC là tam giác vuông tại đỉnh A cạnh BC 3a Chi Tiết
Bạn đang tìm kiếm từ khóa Cho hình chóp sabc có đáy ABC là tam giác vuông tại đỉnh A cạnh BC 3a được Cập Nhật vào lúc : 2022-04-26 07:03:10 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC = a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tại với mặt phẳng (ABC) một góc là 60o. Bán kính mặt cầu ngoại tiếp hình chóp là:
Nội dung chính- Cho hình chóp S.ABC cóđáy ABC là tam giác vuông tại A, , hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của cạnh BC, mặt phẳng (SAB) tạo với mặt đáy một góc bằng . Tính thể tích khối chóp S.ABC theo a.
- Bài tập trắc nghiệm 45 phút Thể tích khối chóp - Khối đa diện và thể tích - Toán Học 12 - Đề số 7
A. a 3
B. a 2
C. a 3 /2
D. a
Cho hình chóp S.ABC cóđáy ABC là tam giác vuông tại A, , hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của cạnh BC, mặt phẳng (SAB) tạo với mặt đáy một góc bằng . Tính thể tích khối chóp S.ABC theo a.
A.
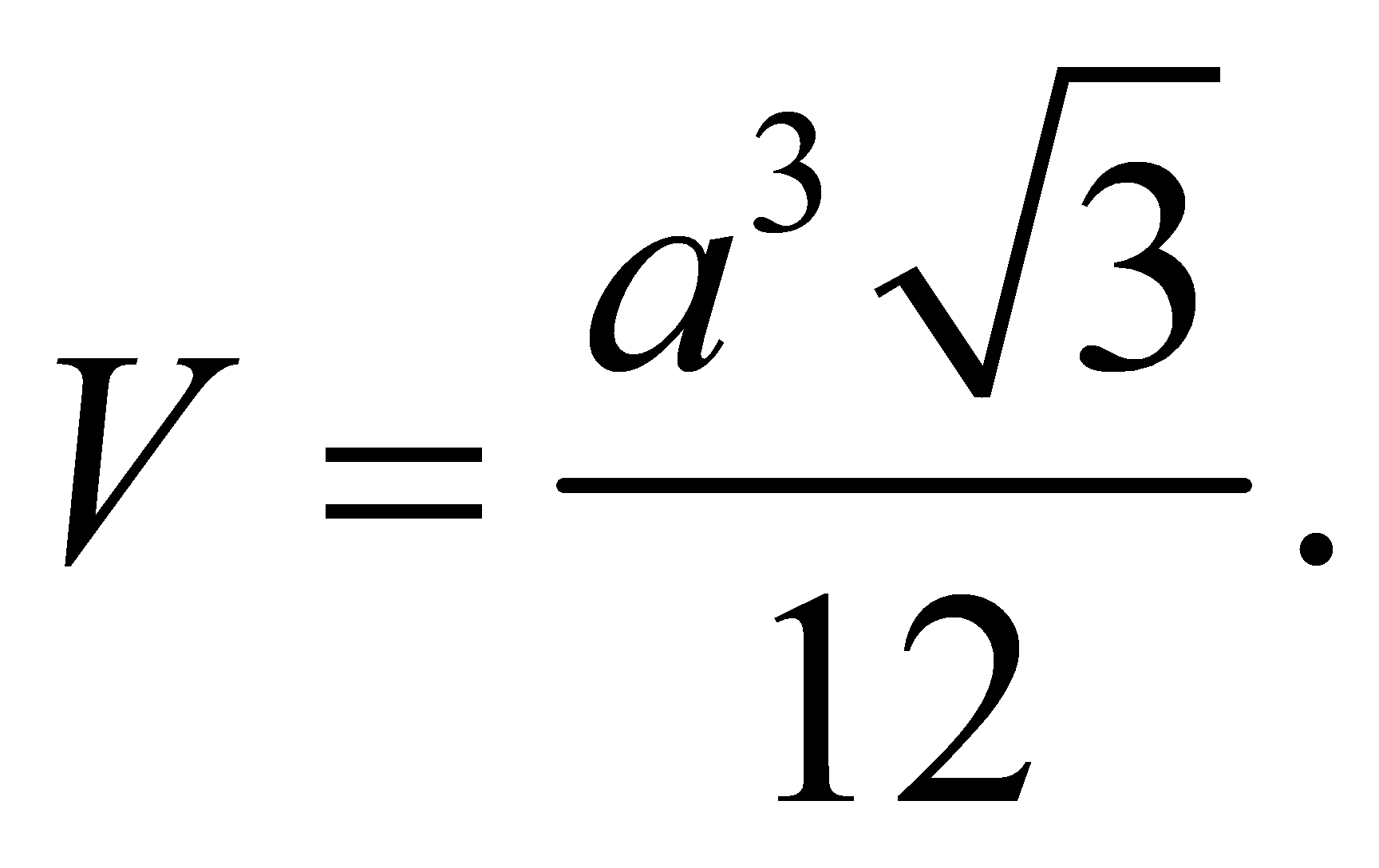
B.
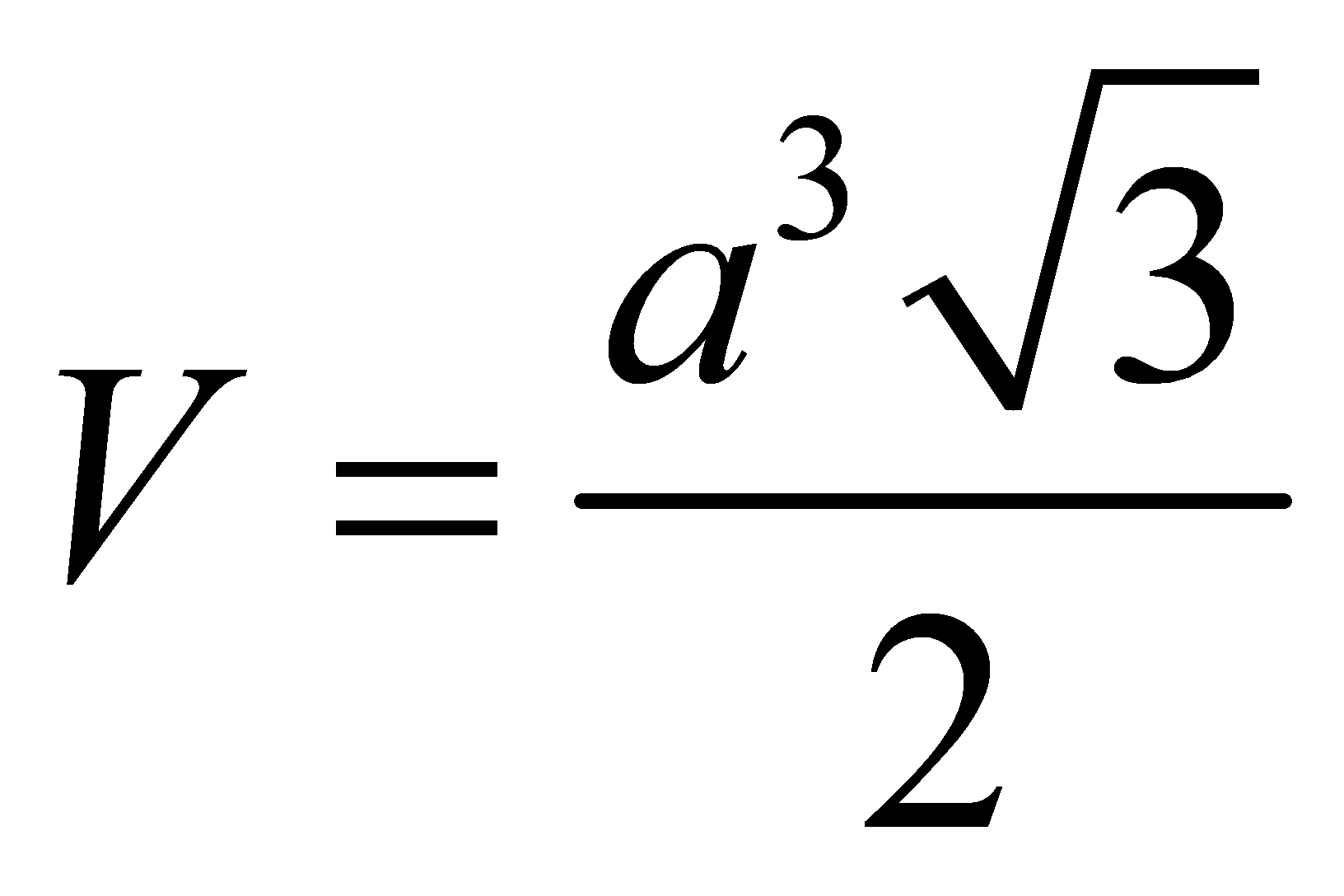
C.
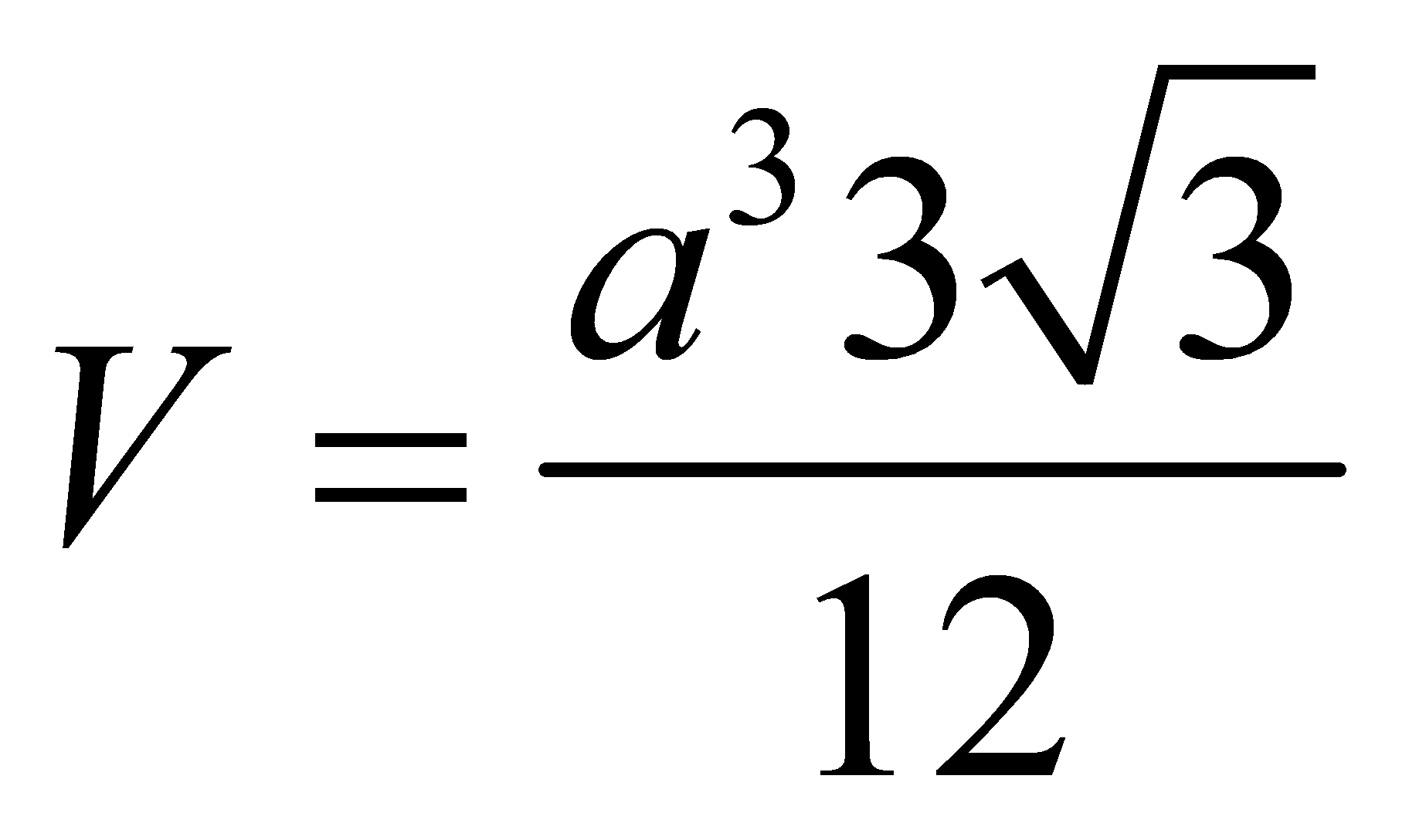
D.
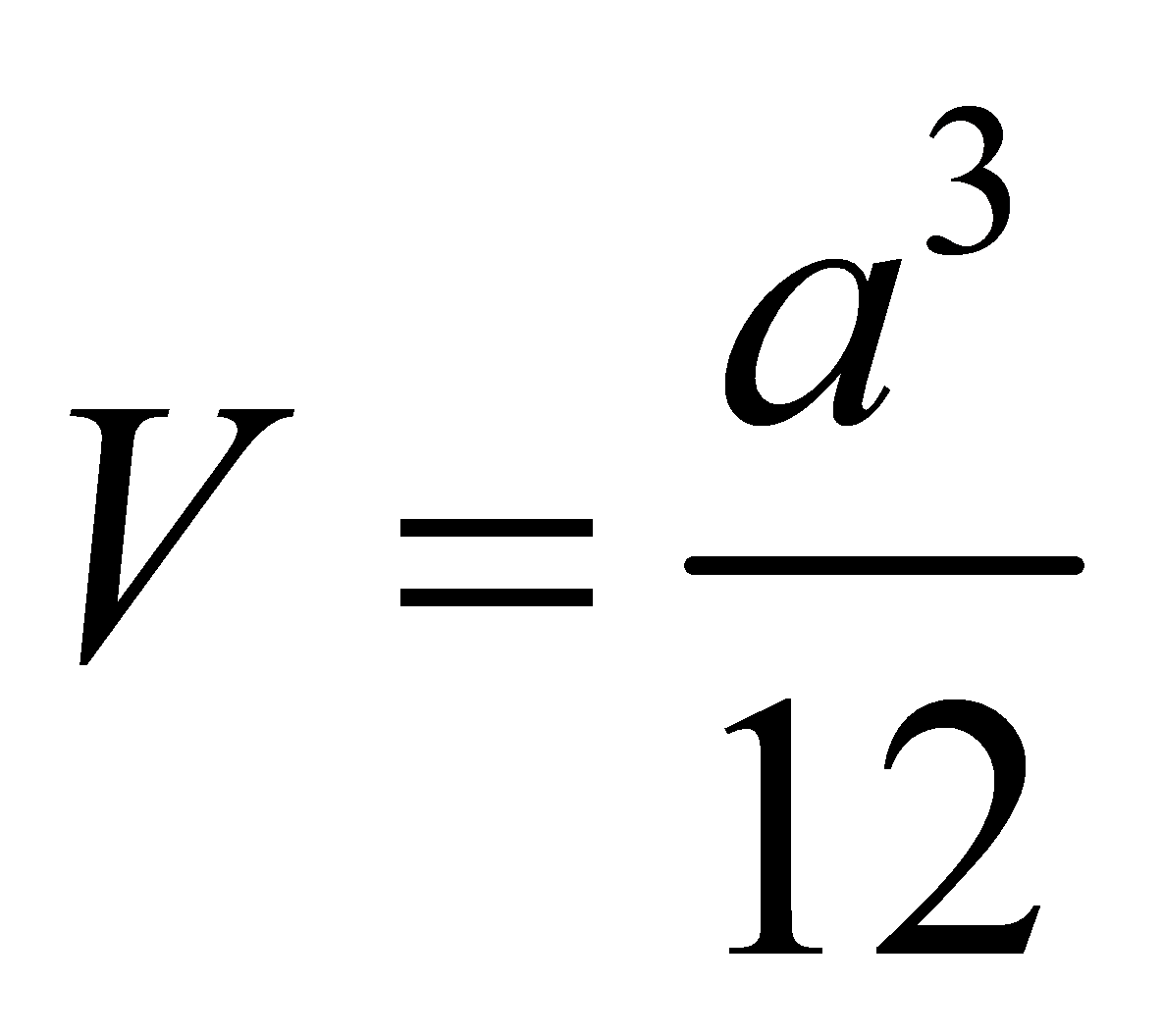
Đáp án và lời giải
Đáp án:A
Lời giải:
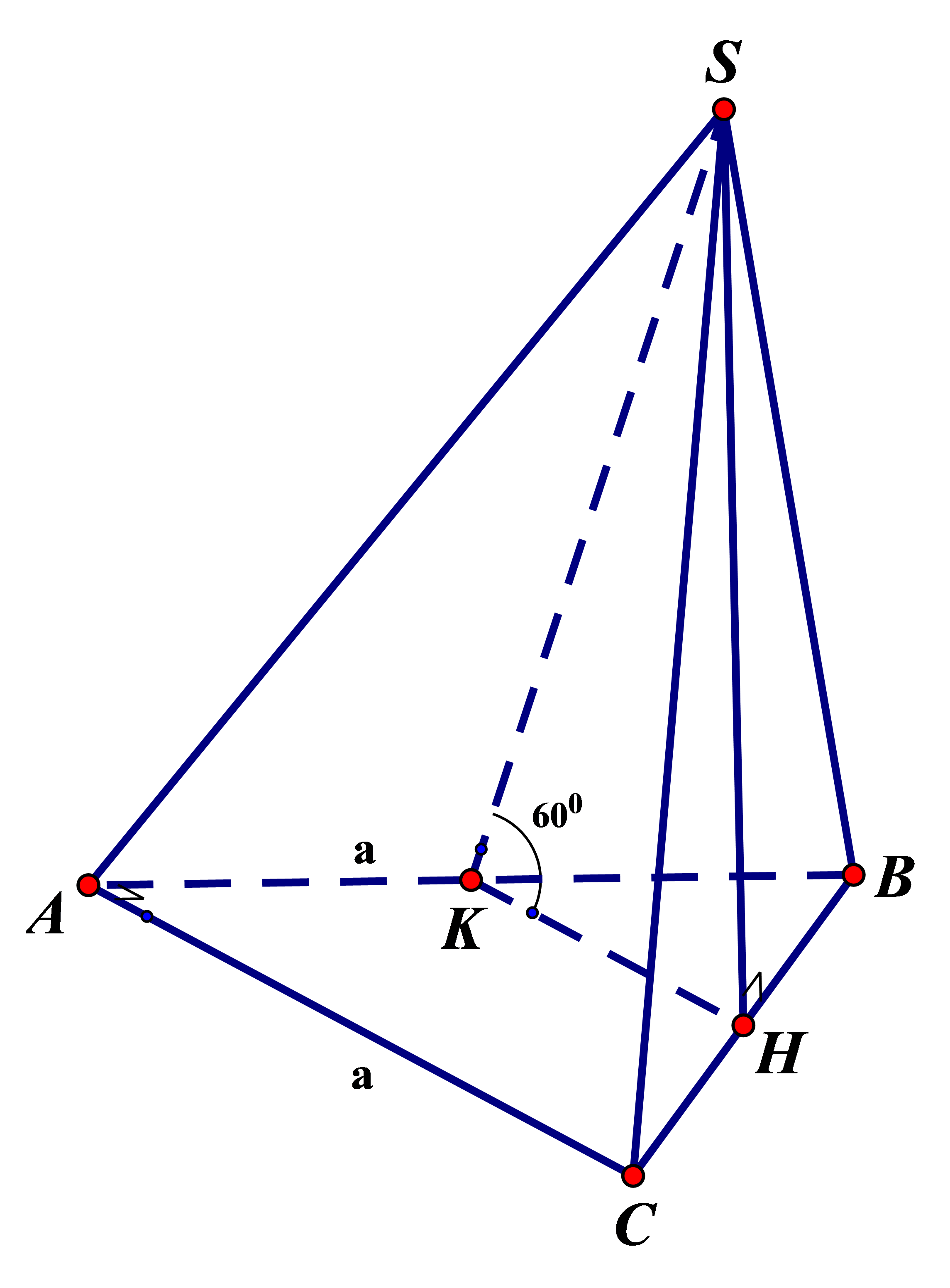 Phân tích: Gọi K là trung điểm của AB
Phân tích: Gọi K là trung điểm của AB 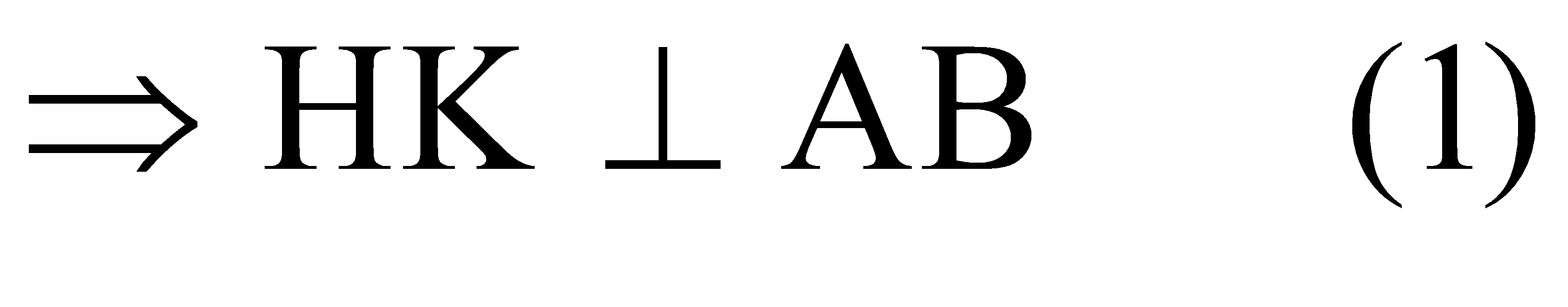 VìSH
VìSH (ABC)nên SH
(ABC)nên SH  AB (2) Từ (1) và (2) suy ra AB
AB (2) Từ (1) và (2) suy ra AB  SK Do đó góc giữa mp(SAB)với đáy bằng góc giữa SK và HK và bằng
SK Do đó góc giữa mp(SAB)với đáy bằng góc giữa SK và HK và bằng 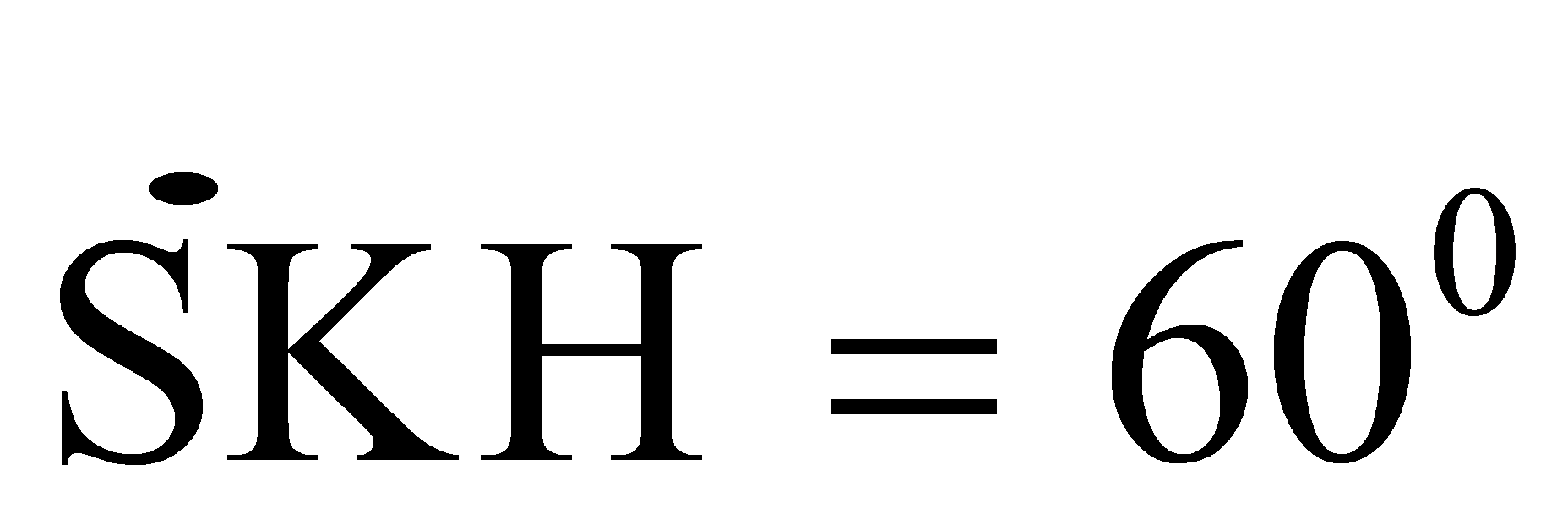 . Áp dụng tỉ số trong tam giác vuông SHK ta tìm kiếm được độ dài đường cao SH. Hướng dẫn giải ĐÁP ÁN A Ta có:
. Áp dụng tỉ số trong tam giác vuông SHK ta tìm kiếm được độ dài đường cao SH. Hướng dẫn giải ĐÁP ÁN A Ta có: 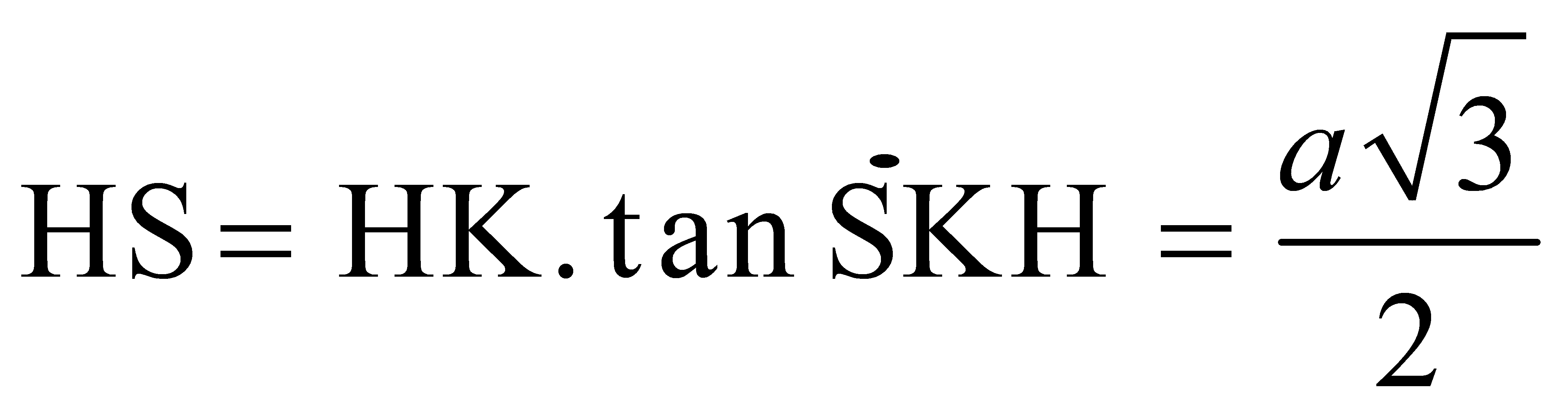
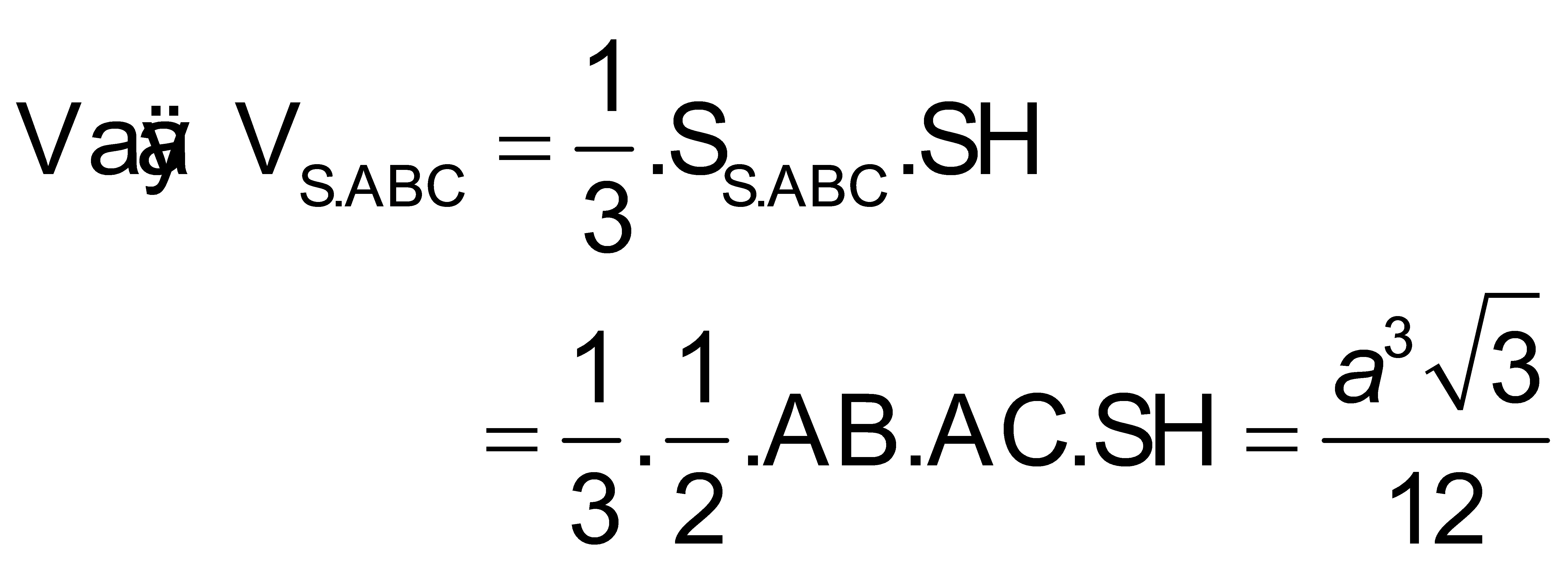 .
.
Vậy đáp án đúng là A.
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 45 phút Thể tích khối chóp - Khối đa diện và thể tích - Toán Học 12 - Đề số 7
Làm bài
Chia sẻ
Một số vướng mắc khác cùng bài thi.
-
Cho hình chóp S.ABCD có đáy là hình chữ nhật với
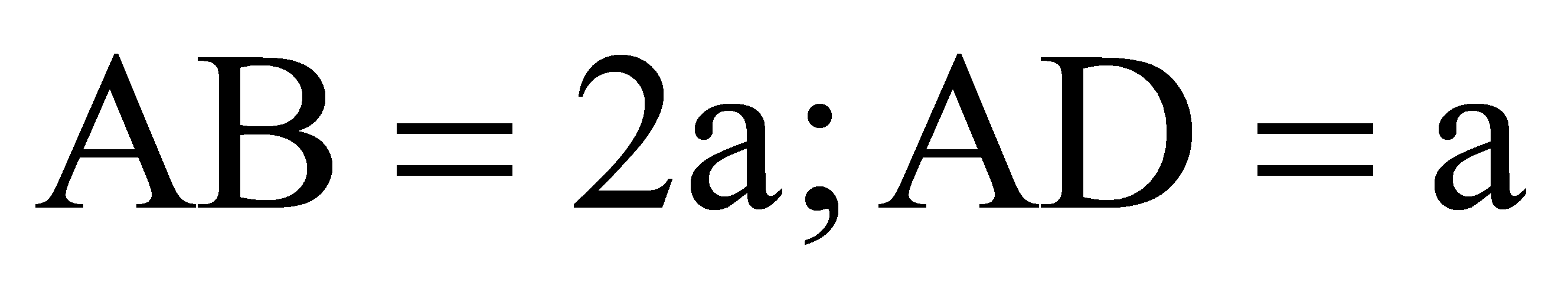 . Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45. Khi đó thể tích khối chóp S.ABCD là:
. Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45. Khi đó thể tích khối chóp S.ABCD là:
-
Cho hình chóp
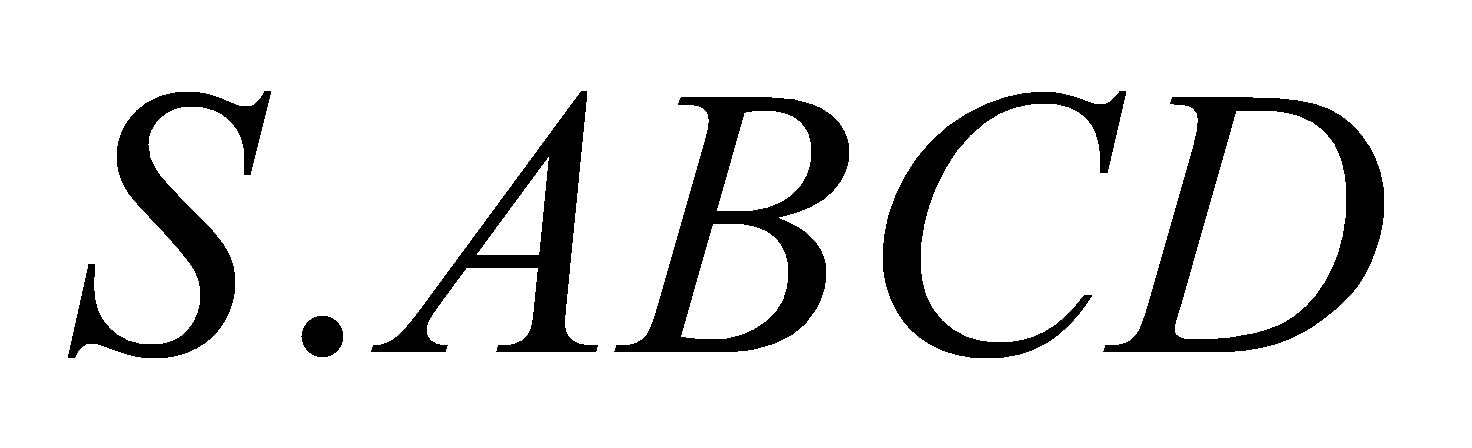 có đáy là hình chữ nhật với
có đáy là hình chữ nhật với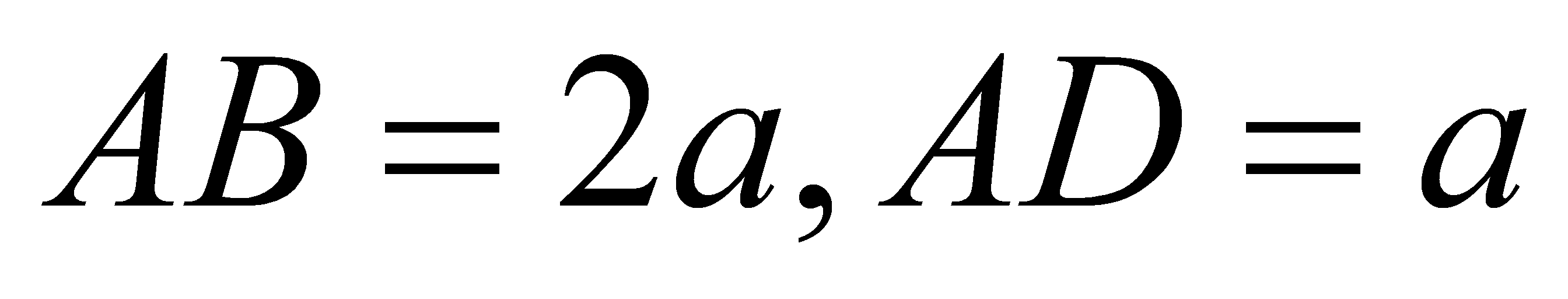 . Hình chiếu của
. Hình chiếu của  lên
lên 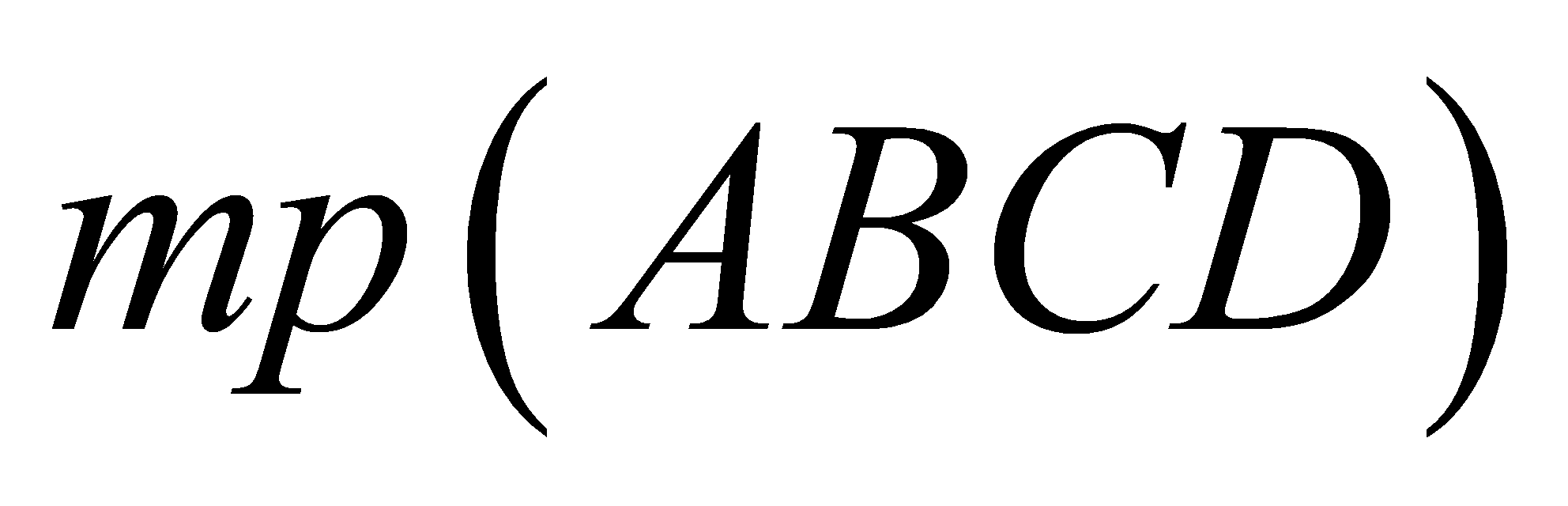 là trung điểm
là trung điểm  của
của 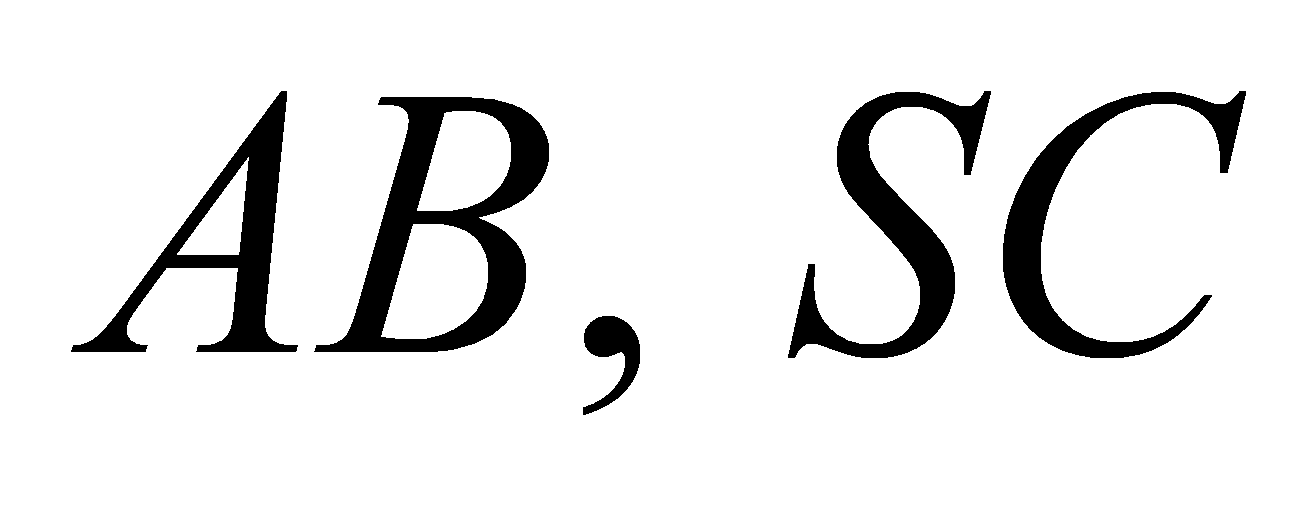 tạo với đáy một góc
tạo với đáy một góc 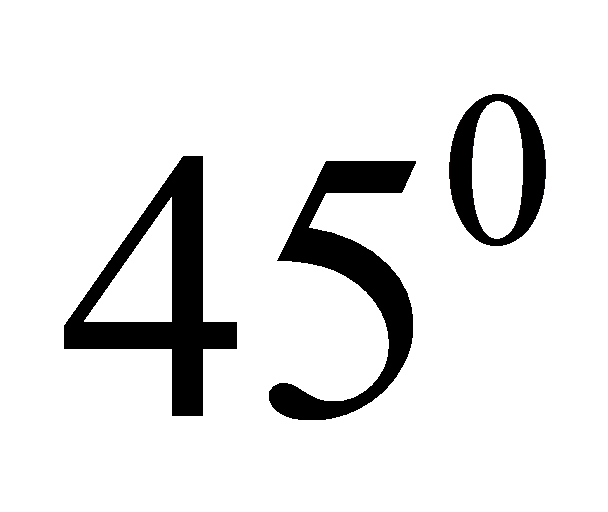 . Thể tích khối chóp
. Thể tích khối chóp 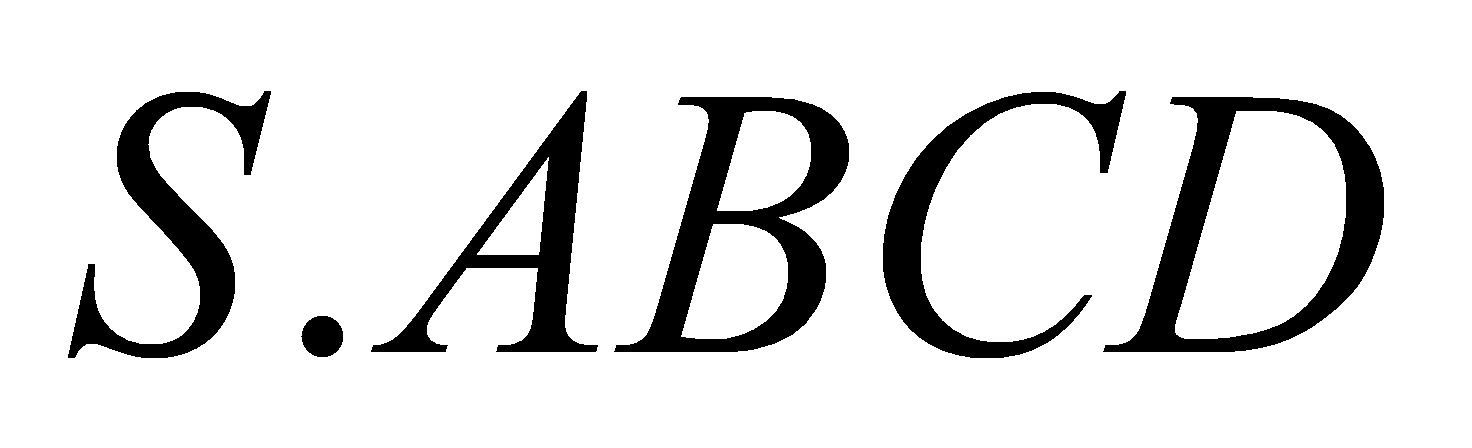 là ?
là ?
-
Cho hình chóp
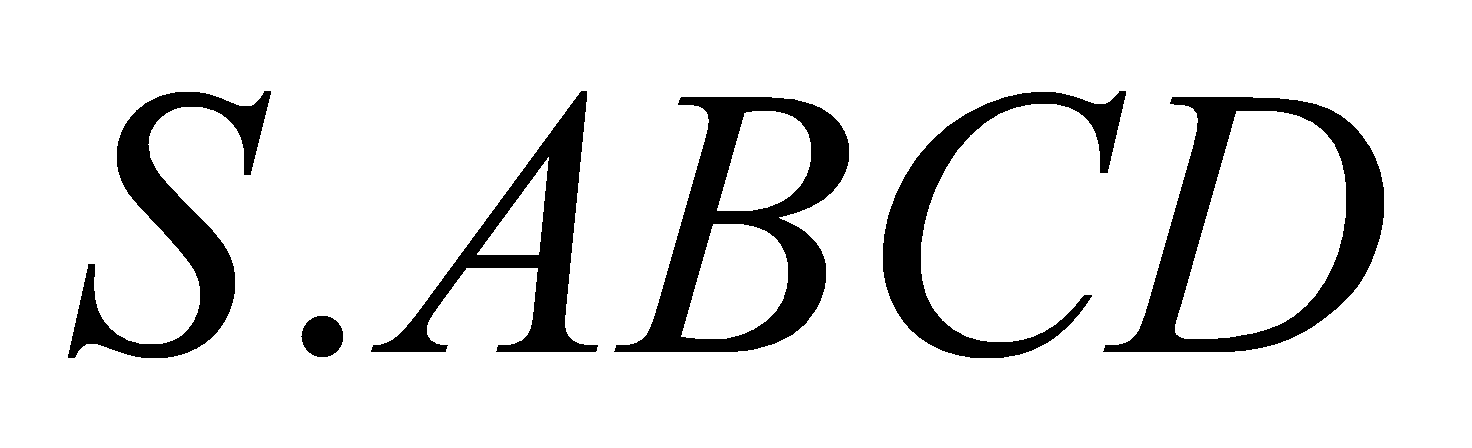 cóđáy
cóđáy 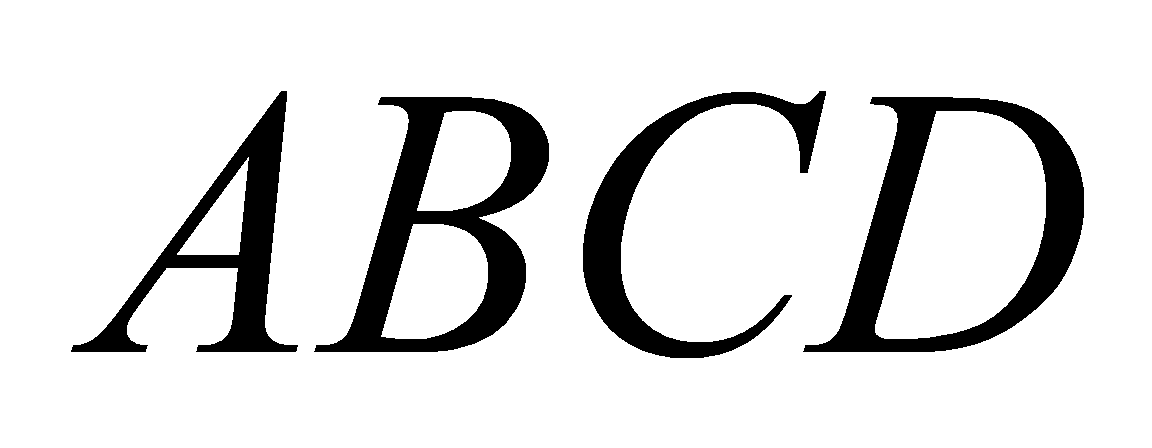 là hình vuông vắn cạnh
là hình vuông vắn cạnh  . Hai mặt bên
. Hai mặt bên  và
và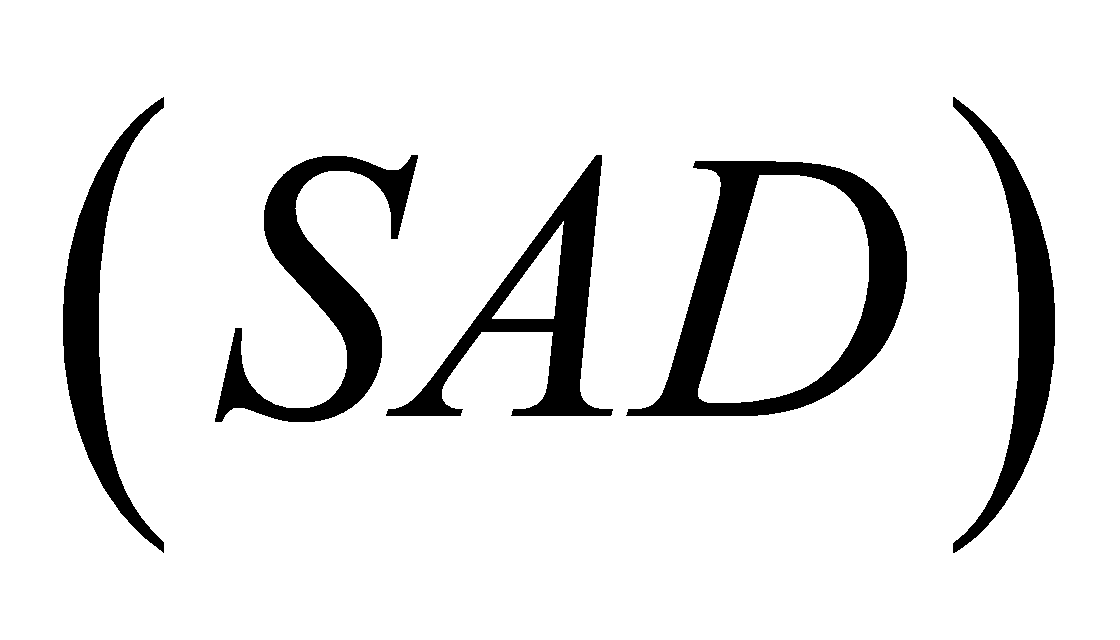 cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng
cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng 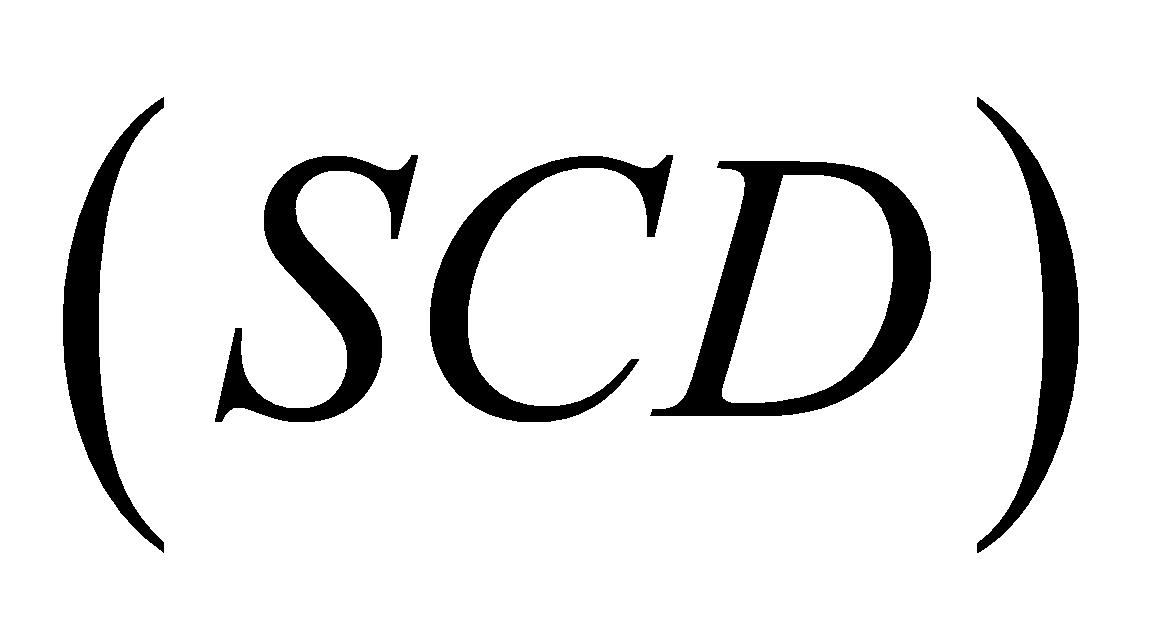 và
và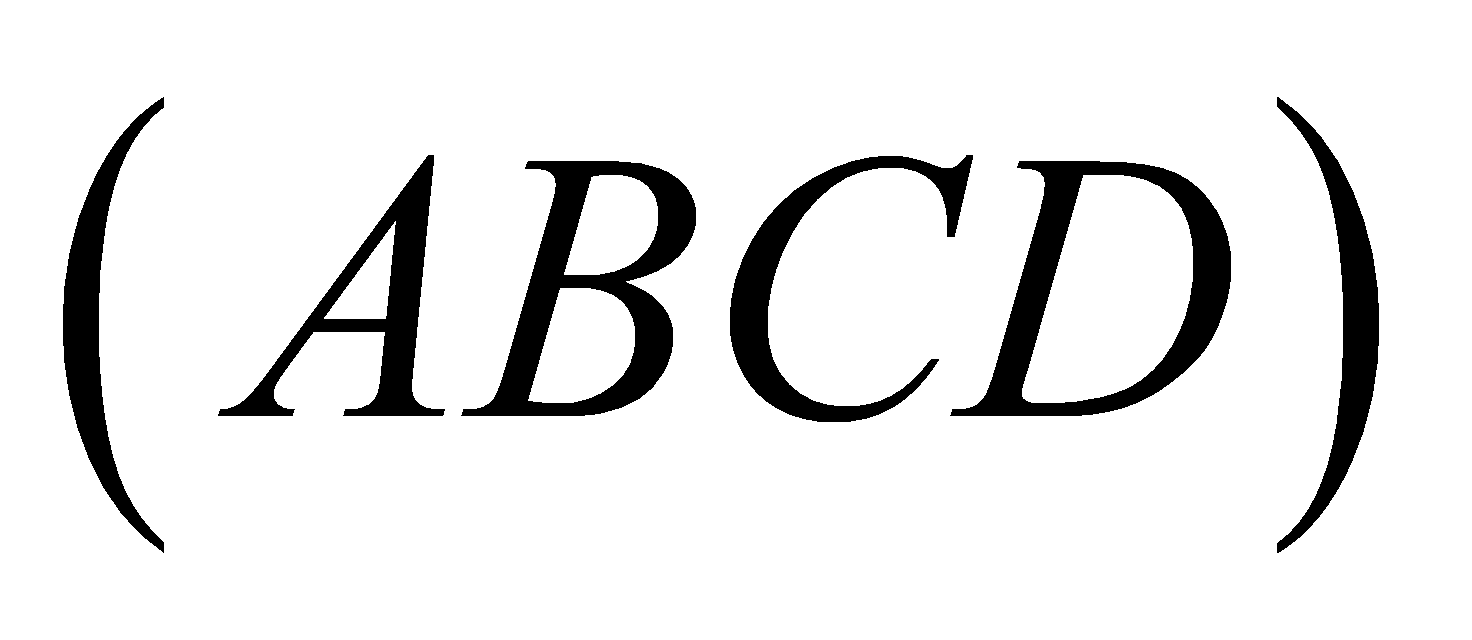 bằng
bằng 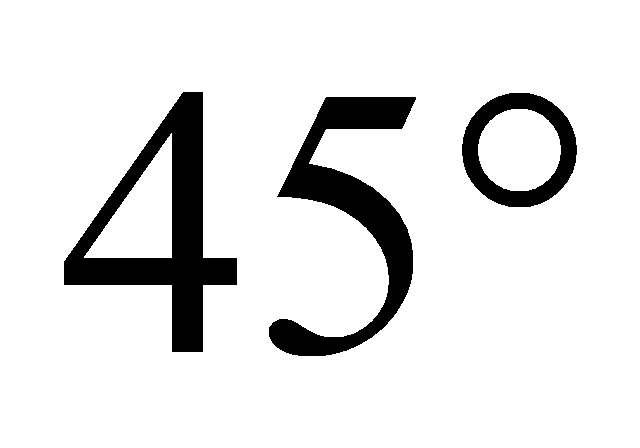 . Gọi
. Gọi 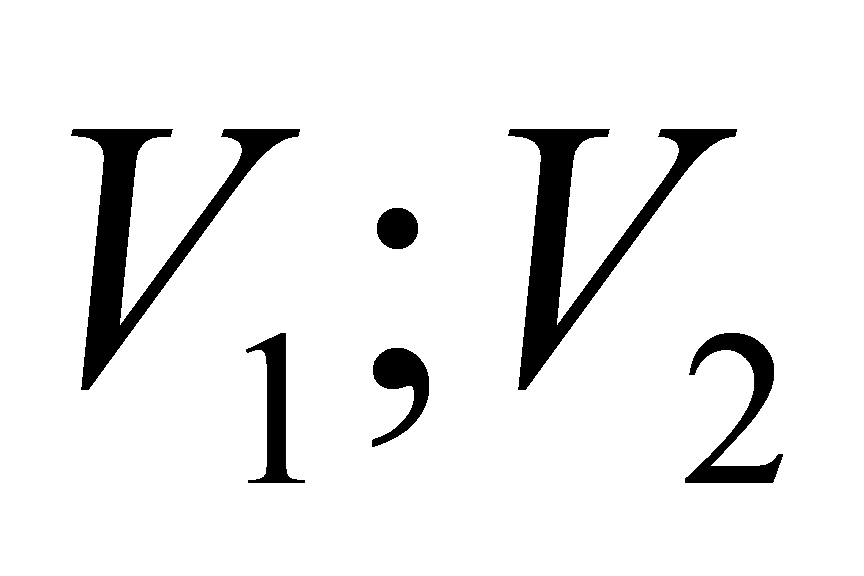 lần lượt là thể tích khối chóp
lần lượt là thể tích khối chóp  và
và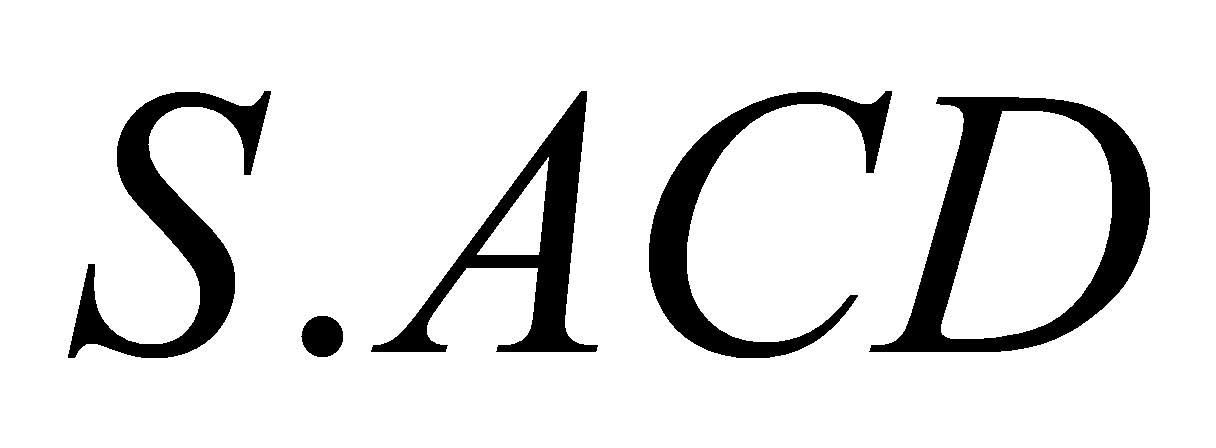 với
với  ,
,  lần lượt là trung điểm của
lần lượt là trung điểm của 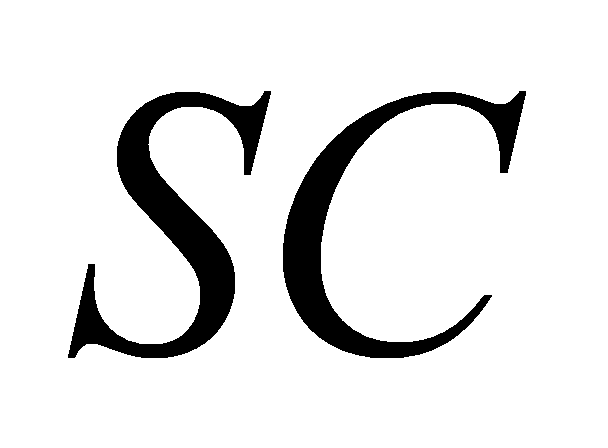 và
và . Tính độ dài đường cao của khối chóp
. Tính độ dài đường cao của khối chóp 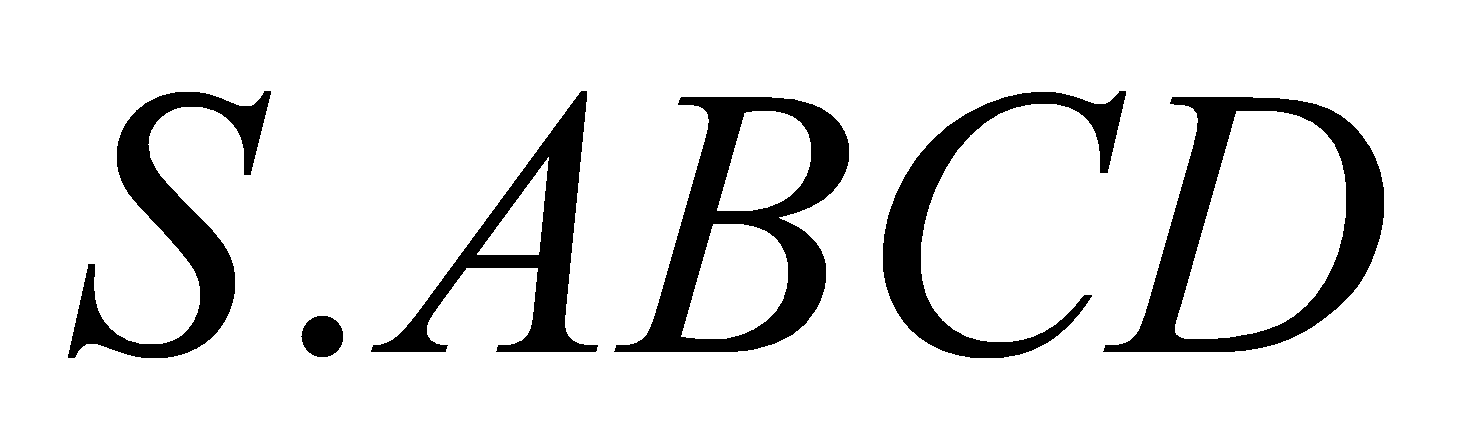 và tỉ số
và tỉ số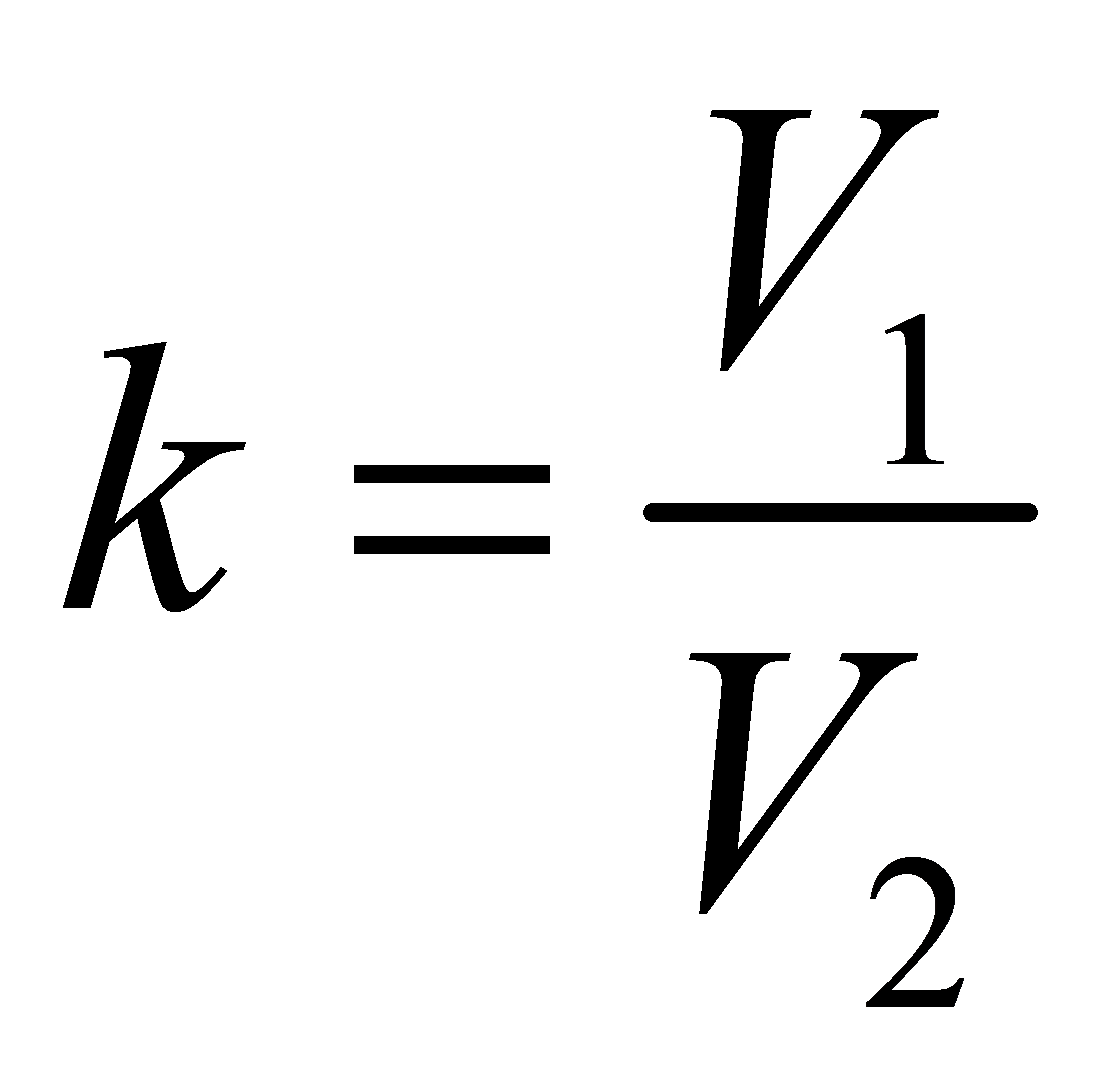 .
.
-
Cho hình chóp
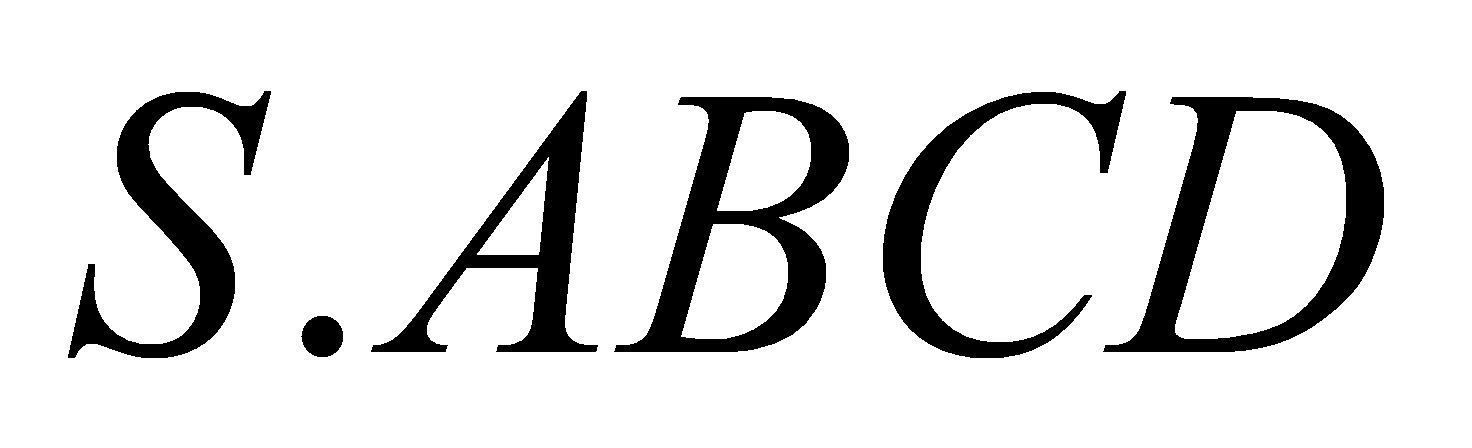 có đáy là hình chữ nhật có chiều rộng
có đáy là hình chữ nhật có chiều rộng  , chiều dài
, chiều dài  , độ cao khối chóp bằng
, độ cao khối chóp bằng  . Thể tích khối chóp theo
. Thể tích khối chóp theo  là?
là?
-
Cho hình chóp S.ABC cóđáy ABC là tam giác vuông tại A,
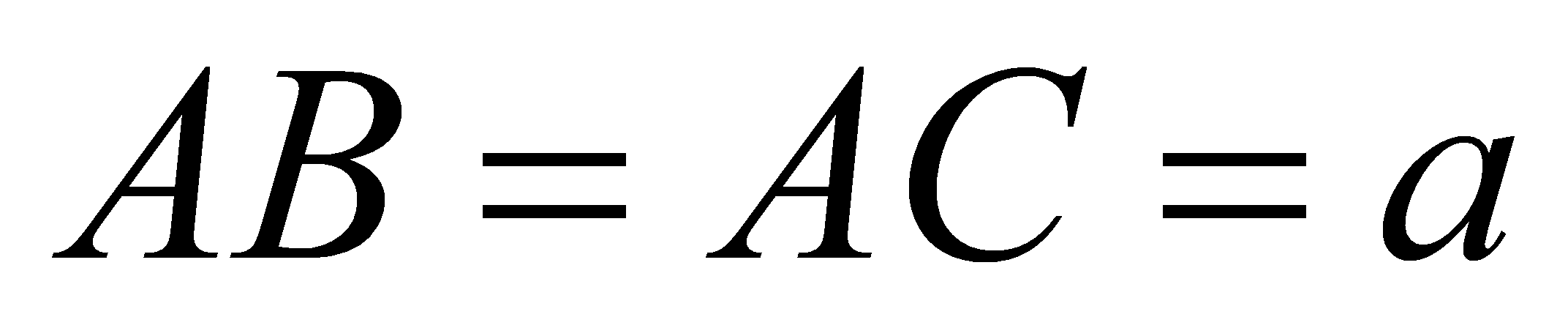 , hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của cạnh BC, mặt phẳng (SAB) tạo với mặt đáy một góc bằng
, hình chiếu vuông góc của đỉnh S trên mặt đáy là trung điểm H của cạnh BC, mặt phẳng (SAB) tạo với mặt đáy một góc bằng  . Tính thể tích khối chóp S.ABC theo a.
. Tính thể tích khối chóp S.ABC theo a.
-
Cho khối tứ diện ABCD hoàn toàn có thể tích V và điểm E trên cạnh AB sao cho
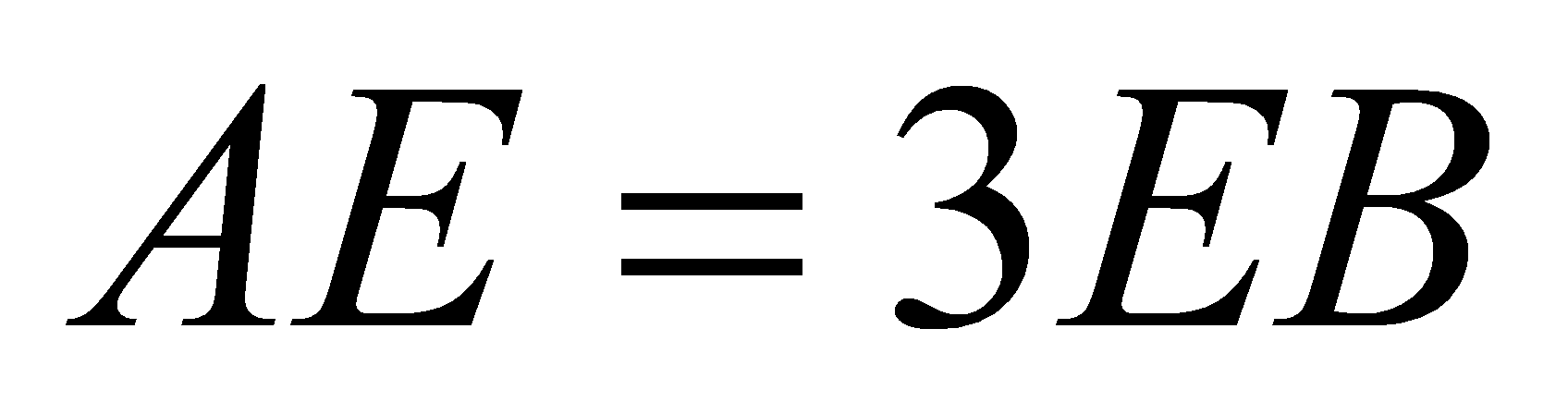 . Tính thể tích khối tứ diện EBCD theo V.
. Tính thể tích khối tứ diện EBCD theo V.
-
Cho khốichóp S.ABC có
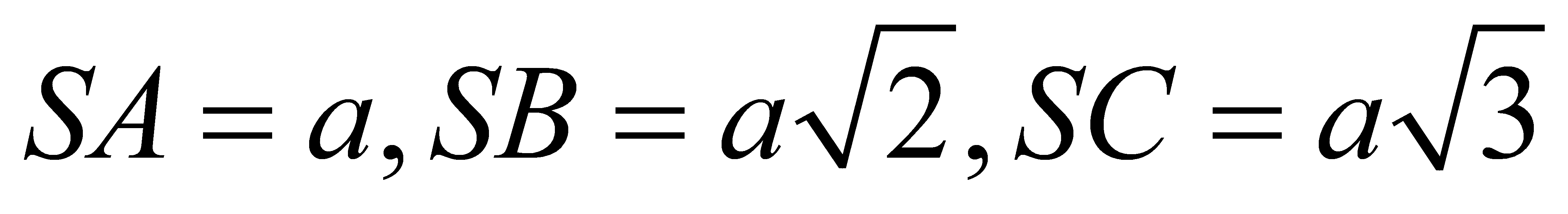 . Thểtíchlớnnhấtcủakhốichóplà:
. Thểtíchlớnnhấtcủakhốichóplà:
-
Cho hìnhchóp
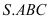 cóđáylàtam giácvuôngcântại
cóđáylàtam giácvuôngcântại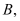
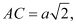
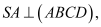
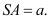 Mặtphẳng
Mặtphẳng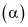 điqua
điqua 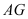 vàsong songvới
vàsong songvới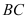 cắt
cắt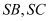 lầnlượttại
lầnlượttại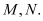 Tínhthểtích
Tínhthểtích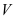 củakhốichóp
củakhốichóp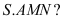
-
Cho một hình chóp tam giác đều phải có cạnh bằng
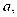 góc giữa cạnh bên và mặt phẳng đáy bằng
góc giữa cạnh bên và mặt phẳng đáy bằng  Thể tích khối chóp đó là
Thể tích khối chóp đó là
-
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông vắn cạnh
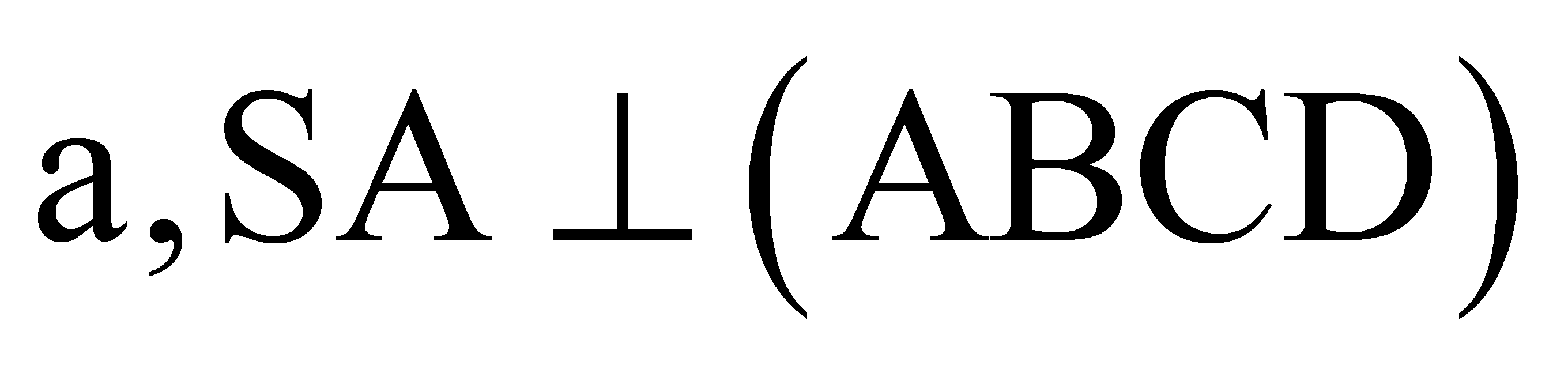 và
và 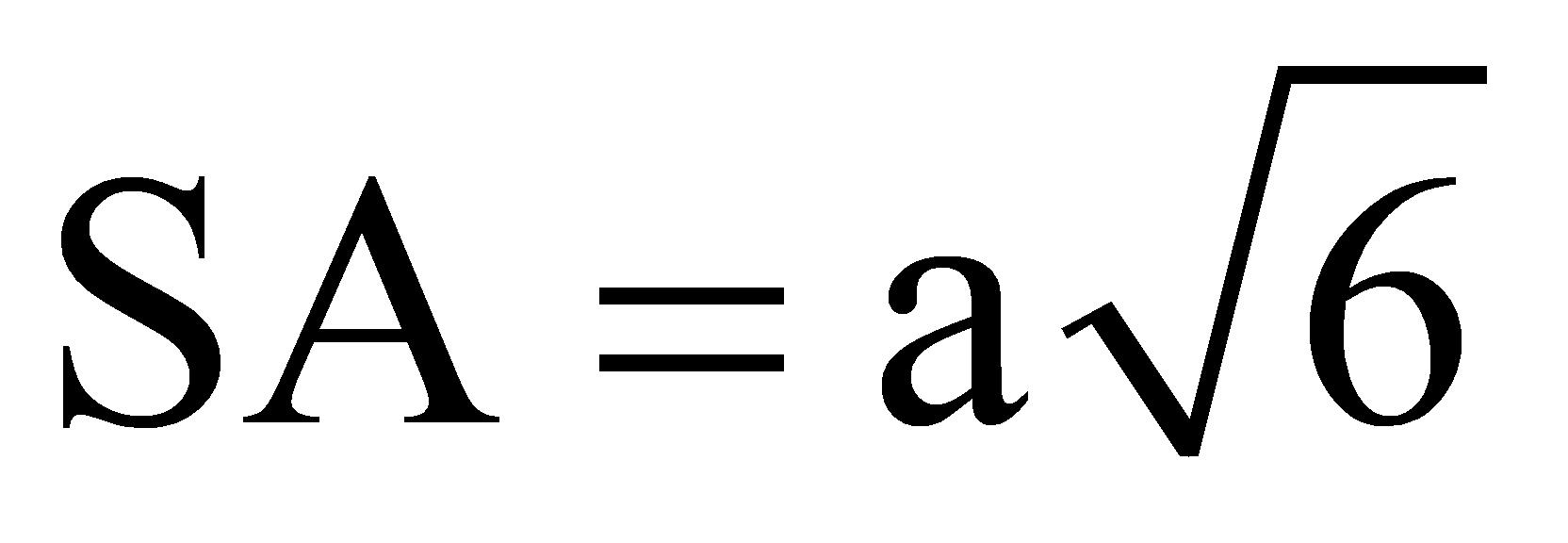 . Thể tích của khối chóp S/ABCD bằng:
. Thể tích của khối chóp S/ABCD bằng:
-
Hình chóp
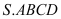 có đáy
có đáy 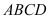 là hình vuông vắn cạnh
là hình vuông vắn cạnh 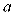 , hình chiếu vuông góc của
, hình chiếu vuông góc của 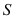 trên mặt phẳng
trên mặt phẳng 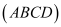 trùng với trung điểm của
trùng với trung điểm của 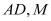 là trung điểm của
là trung điểm của 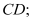 cạnh bên
cạnh bên 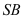 phù thích hợp với đáy một góc
phù thích hợp với đáy một góc  . Thể tích của khối chóp
. Thể tích của khối chóp 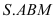 là
là
-
Cho hình chóp S.ABCDcó đáy ABCDlà hình vuông vắn cạnh a, hình chiếu vuông góc của Strên mặt phẳng (ABCD) là yếu tố Hthuộc cạnh ADsao cho HD = 2HA. Biết góc giữa SBvà mặt phẳng (ABCD) bằng 300. Tính theo athể tích của khối chóp S.ABCDlà
-
Cho khối tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau và
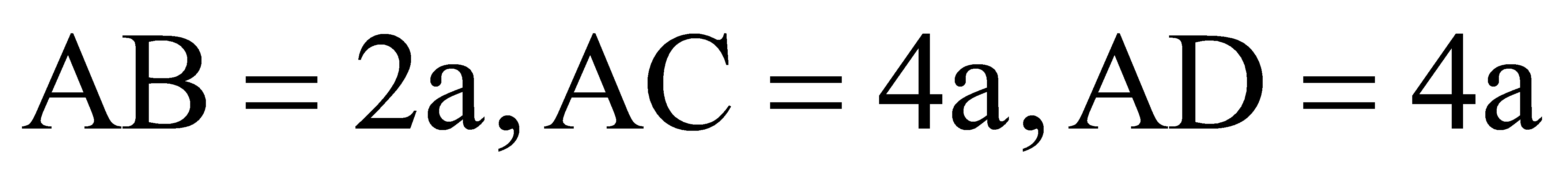 . Gọi H, K lần lượt là hình chiếu của A lên BC và BD . Thể tích của khối tứ diện ABHK là:
. Gọi H, K lần lượt là hình chiếu của A lên BC và BD . Thể tích của khối tứ diện ABHK là:
-
Kíhiệu V làthểtíchcủakhốihộpABCD. A’B’C’D’; V1làthểtíchcủakhốitứdiệnB’D’AC. Mệnhđềnàođúng?
-
Cho hình lăng trụ
 có đáy ABC là tam giác vuông cân đỉnh C, cạnh góc vuông bằng
có đáy ABC là tam giác vuông cân đỉnh C, cạnh góc vuông bằng  , độ cao bằng
, độ cao bằng  . G là trọng tâm tam giác
. G là trọng tâm tam giác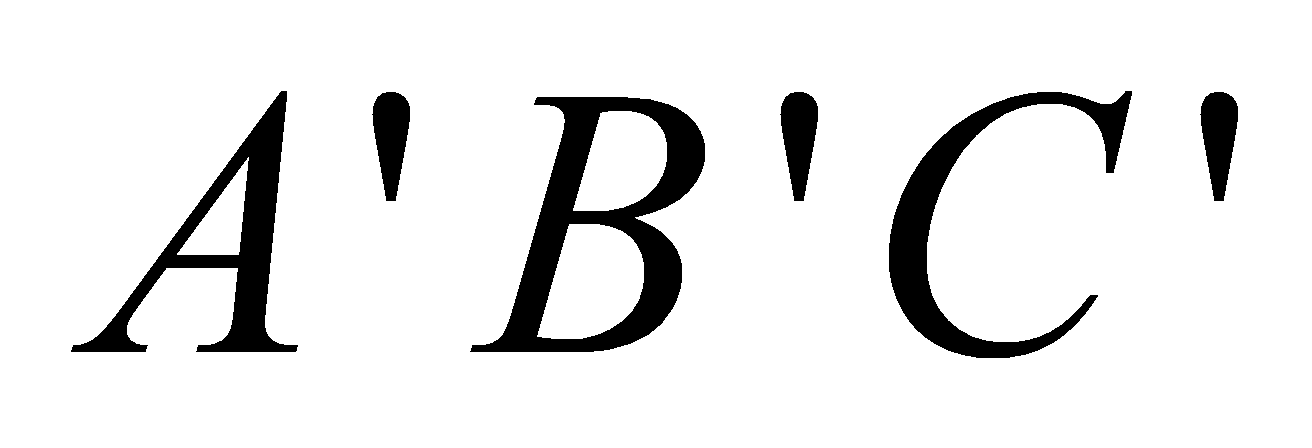 . Thể tích khối chóp
. Thể tích khối chóp 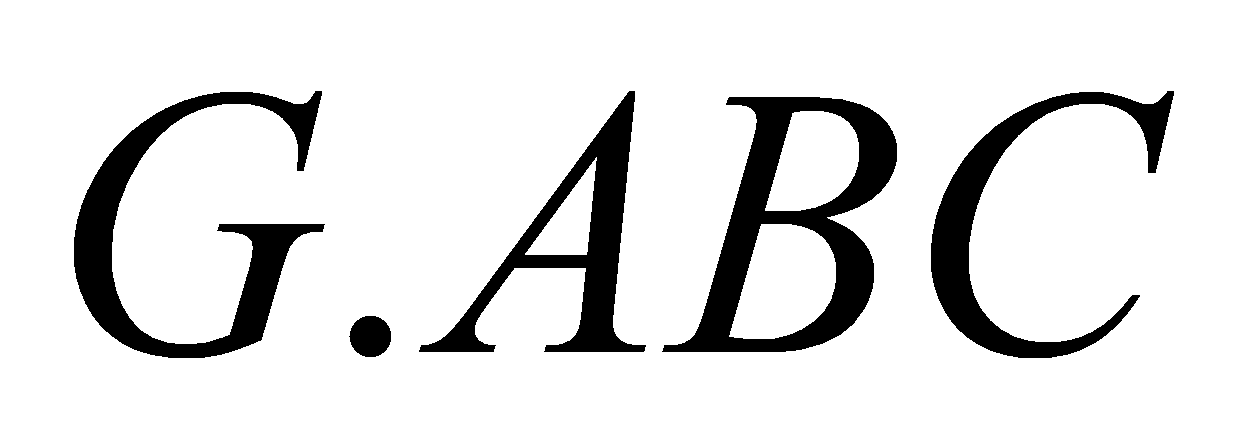 là:
là:
-
Cho hình chóp
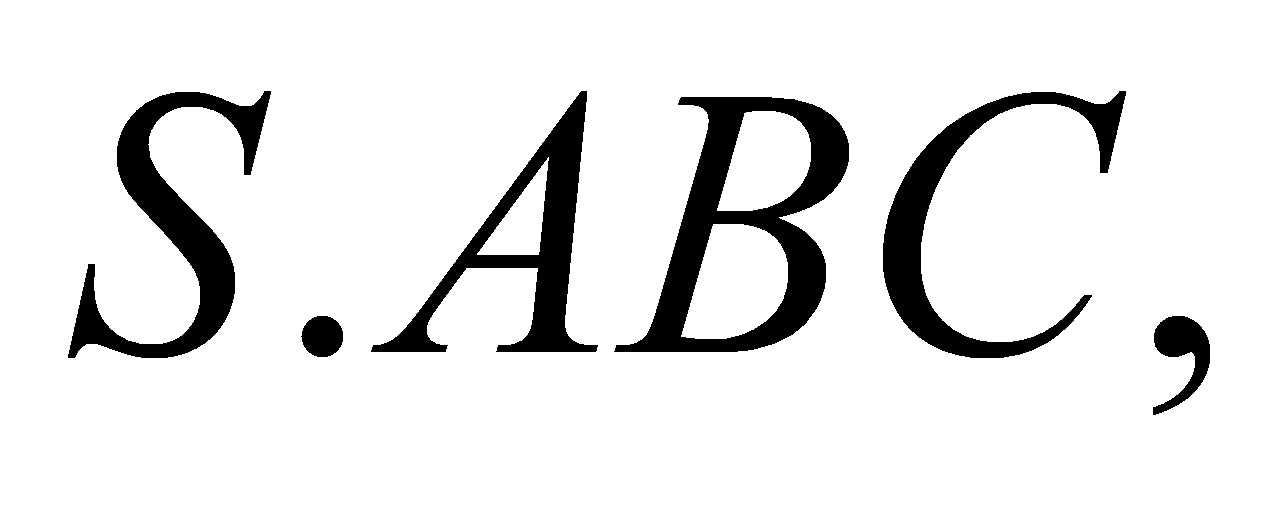 có đáy ABC là tam giác đều cạnh
có đáy ABC là tam giác đều cạnh  Các mặt bên
Các mặt bên 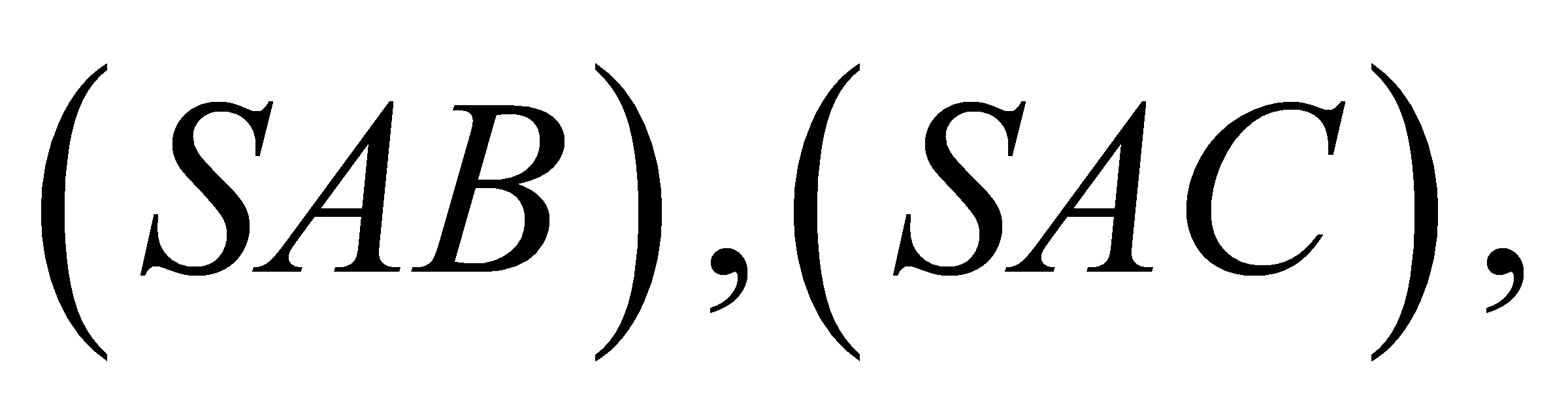
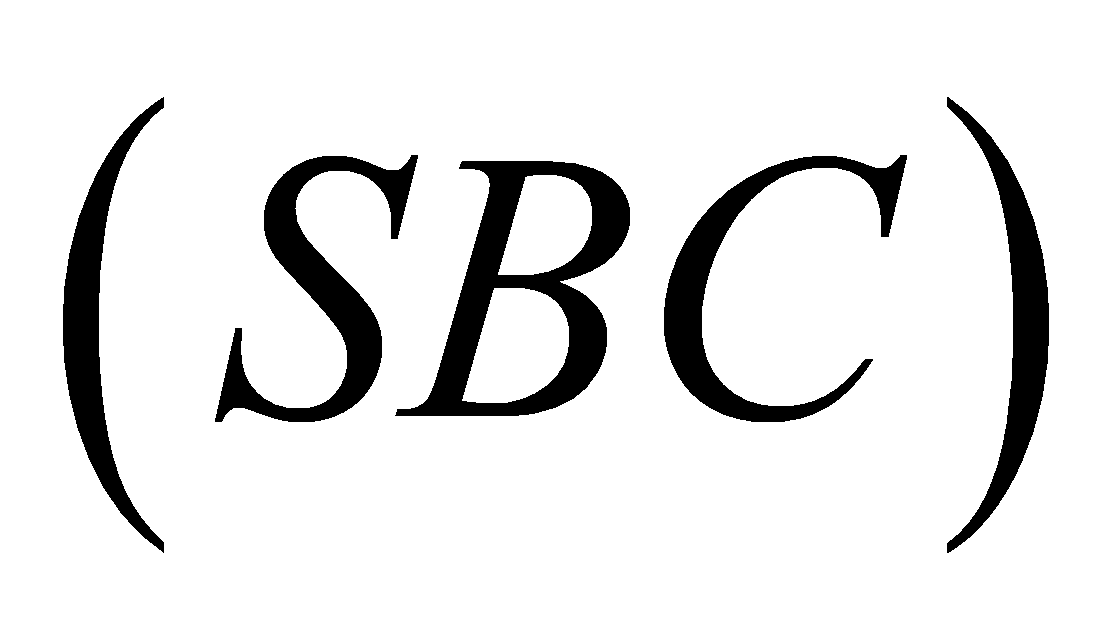 lần lượt tạo với đáy những góc lần lượt là
lần lượt tạo với đáy những góc lần lượt là 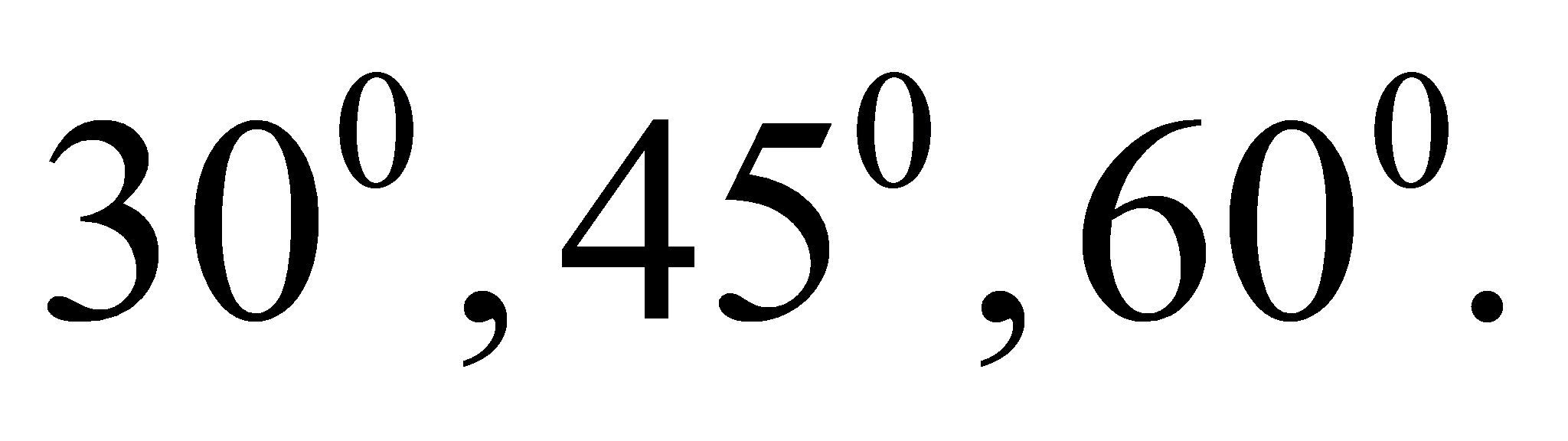 Tính thể tích V của khối chóp
Tính thể tích V của khối chóp 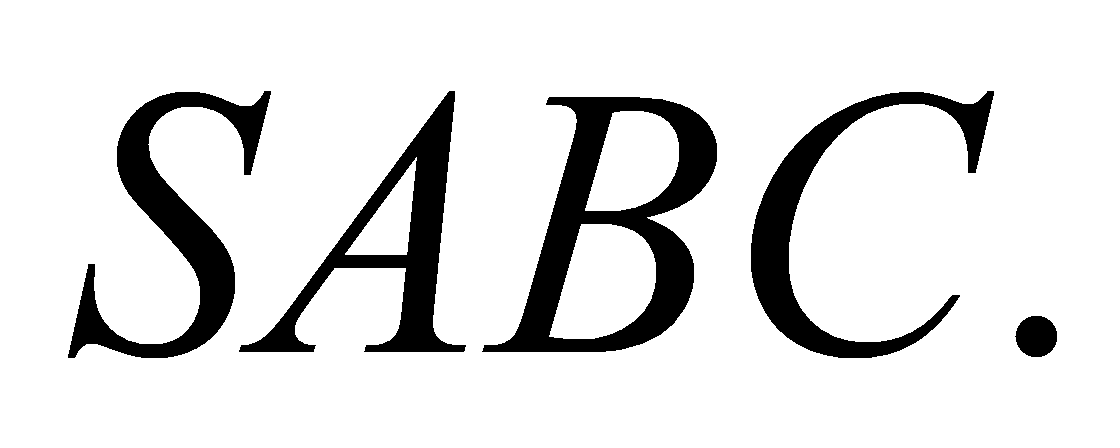 Biết rằng hình chiếu vuông góc của S trên mặt phẳng
Biết rằng hình chiếu vuông góc của S trên mặt phẳng 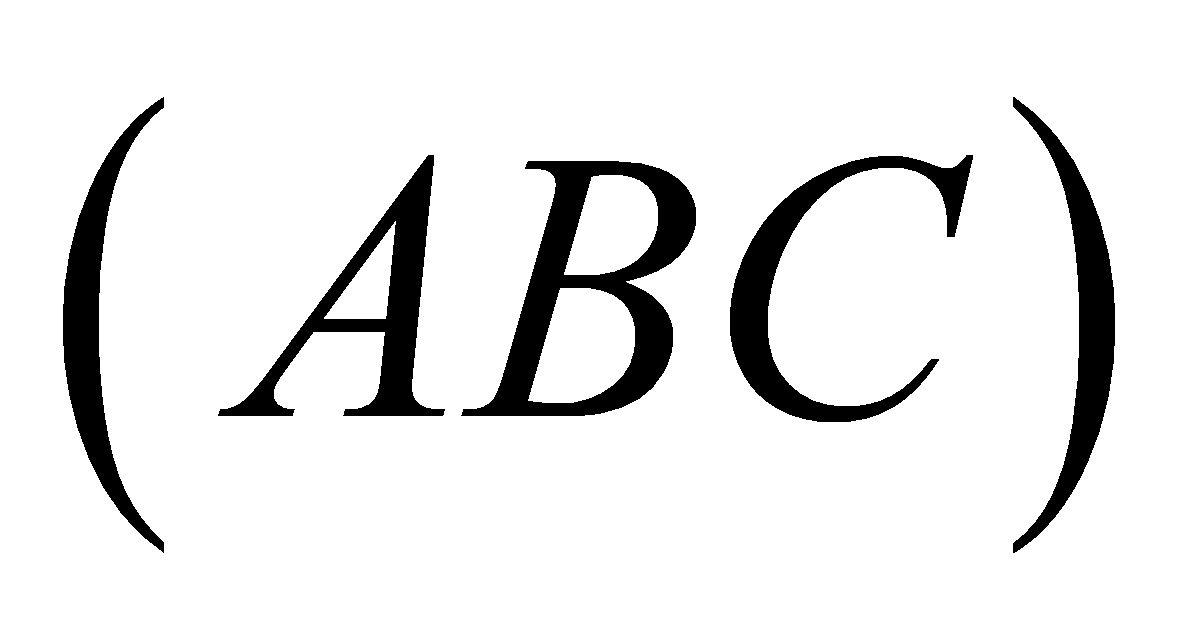 nằm bên cạnh trong tam giác
nằm bên cạnh trong tam giác 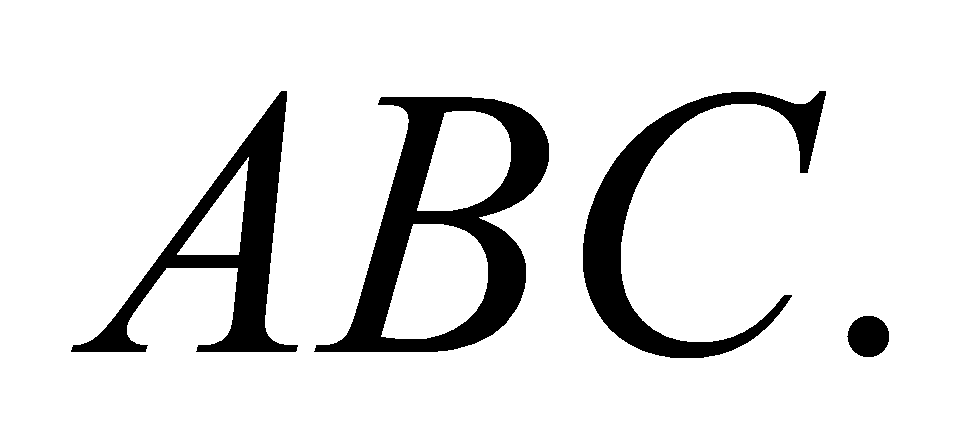
-
Cho hình chóp. tứ giác đều
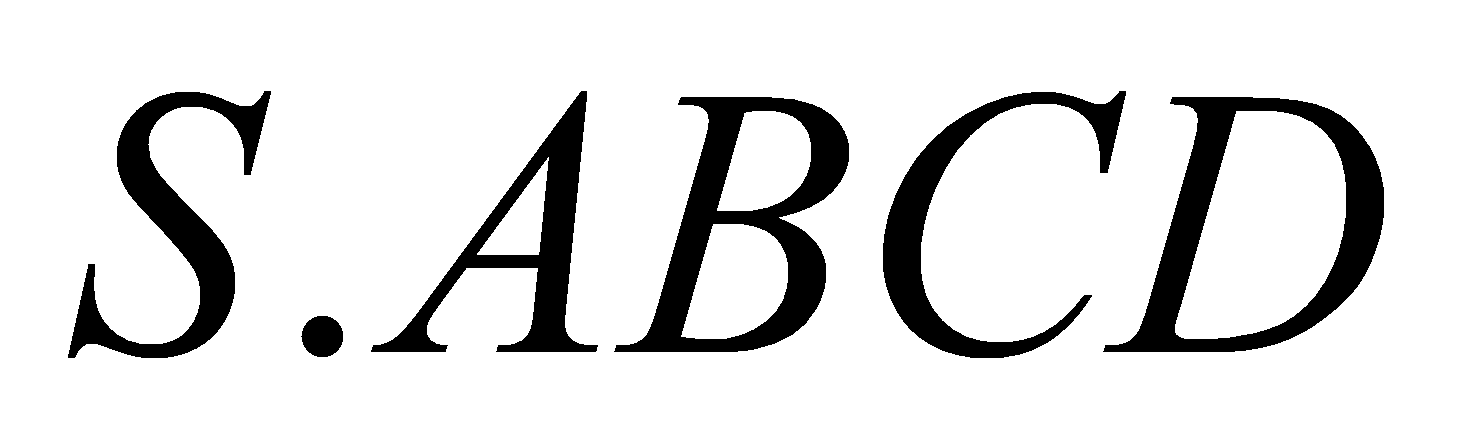 ,
,  là giao điểm của
là giao điểm của 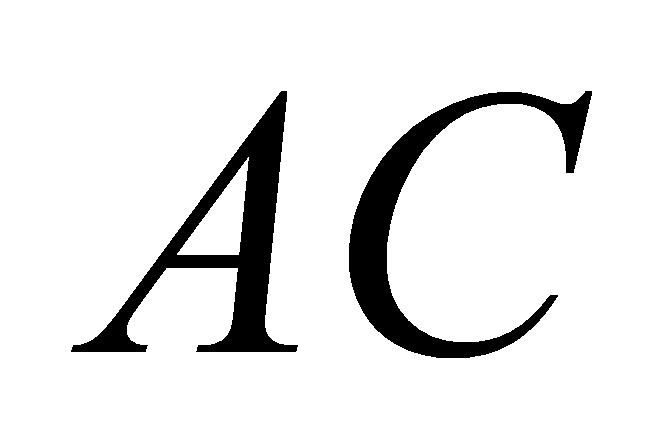 và
và 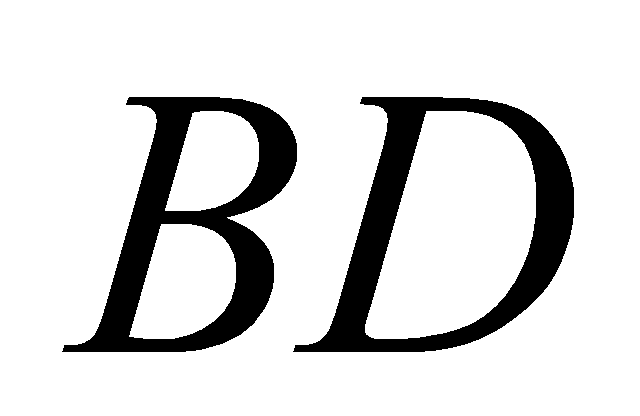 . Biết mặt bên của hình chóp là tam giác đều và khoảng chừng từ
. Biết mặt bên của hình chóp là tam giác đều và khoảng chừng từ  đến mặt bên là
đến mặt bên là . Tínhthểtíchkhốichóp
. Tínhthểtíchkhốichóp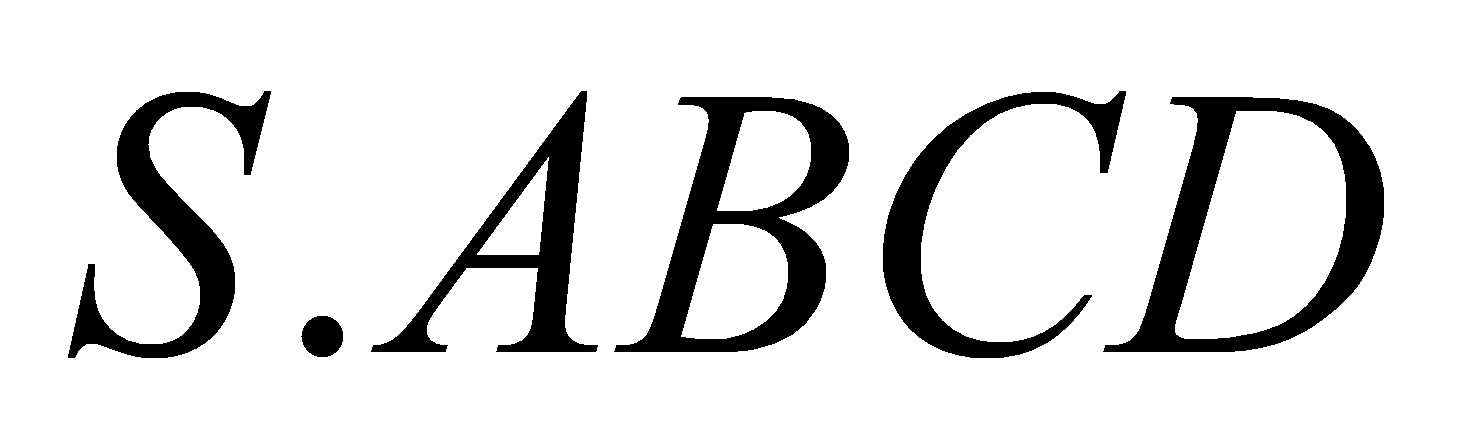 theo
theo .
.
-
Cho khối chóp S.ABC có SA vuông góc với mp (ABC) , tam giác ABC vuông tại B, BC = a, góc
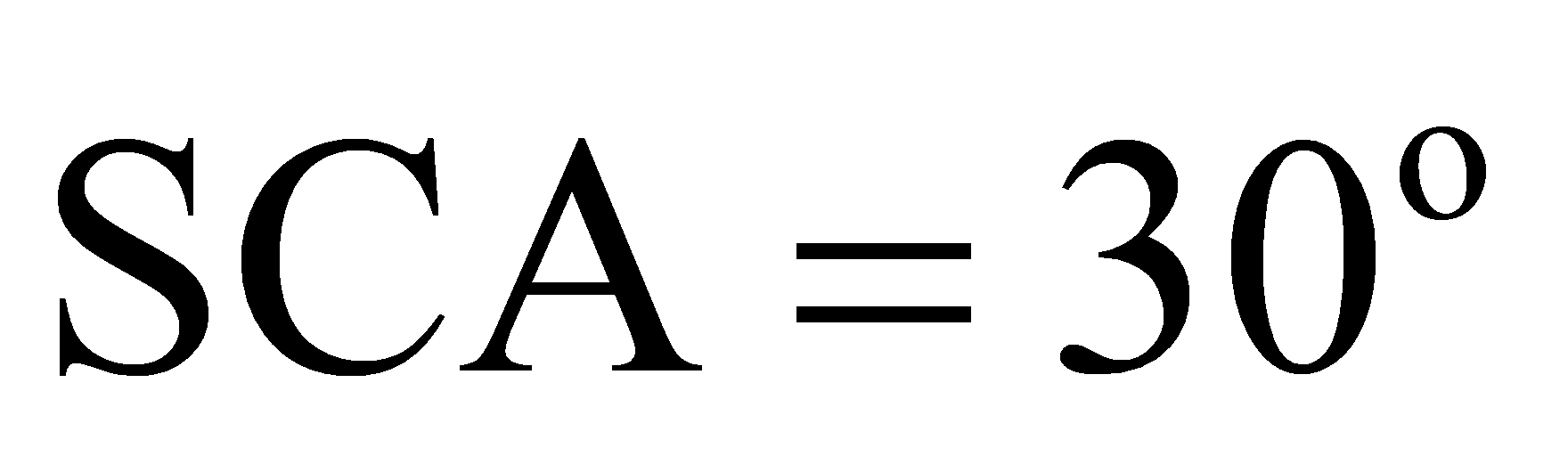 góc
góc 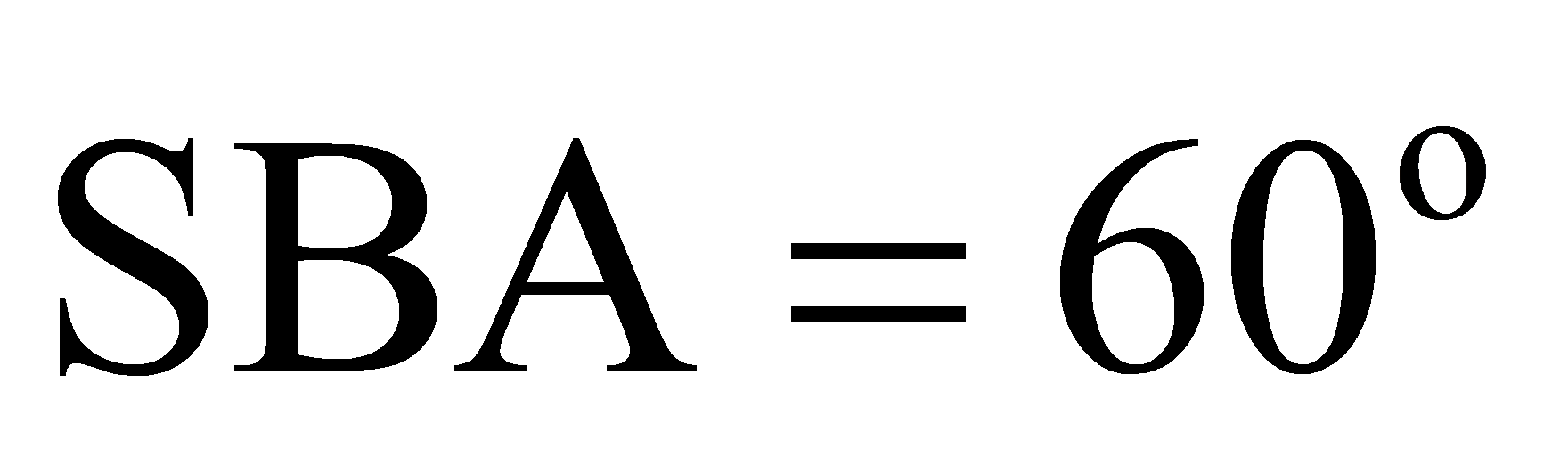 . Thể tích khối chóp là ?
. Thể tích khối chóp là ?
-
Cho hình chóp
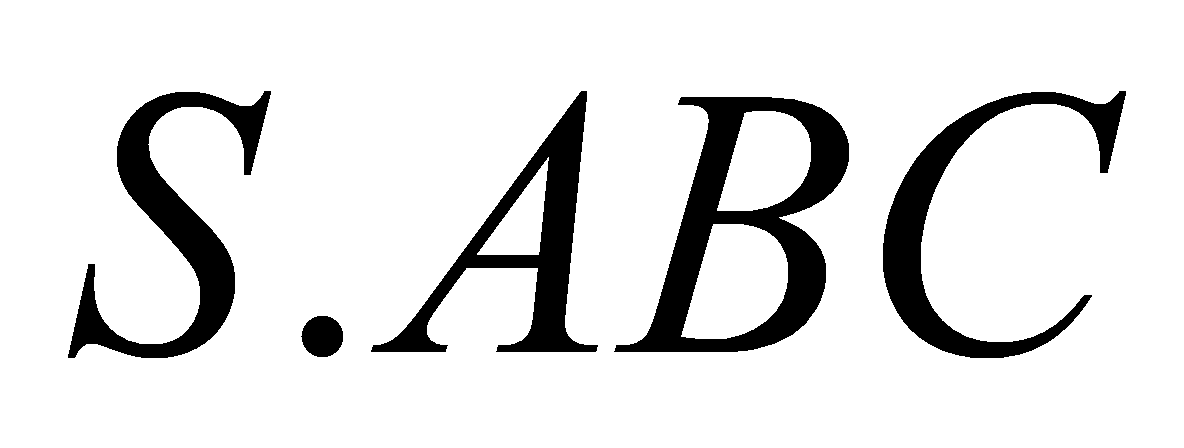 có đáy
có đáy 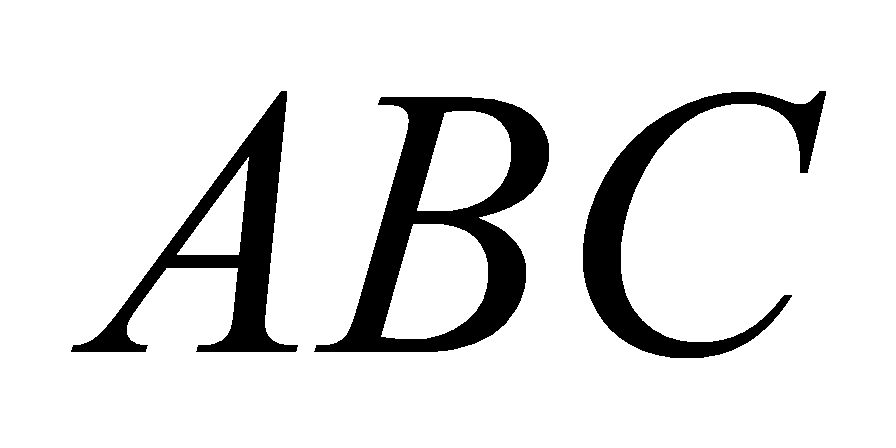 là tam giác vuông cân tại
là tam giác vuông cân tại  ,
, 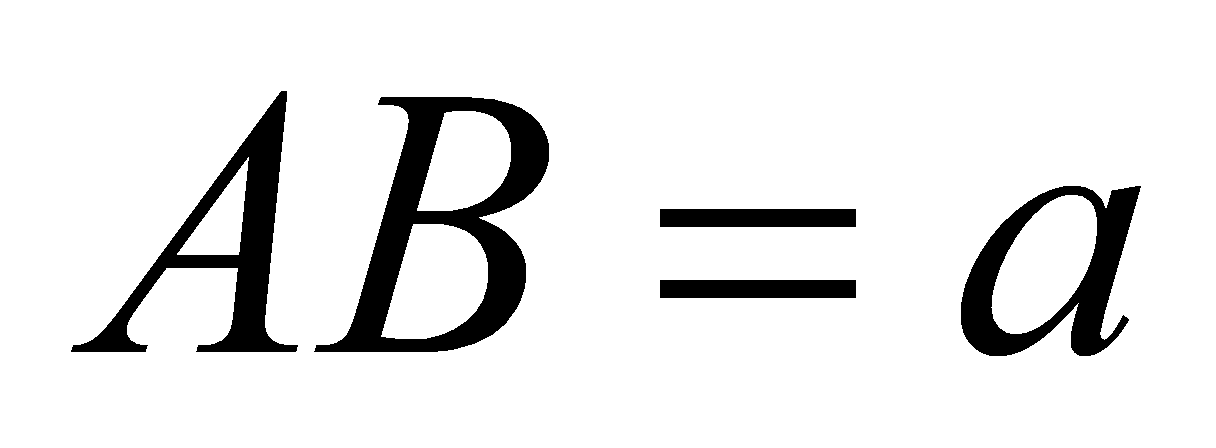 . Cạnh bên
. Cạnh bên 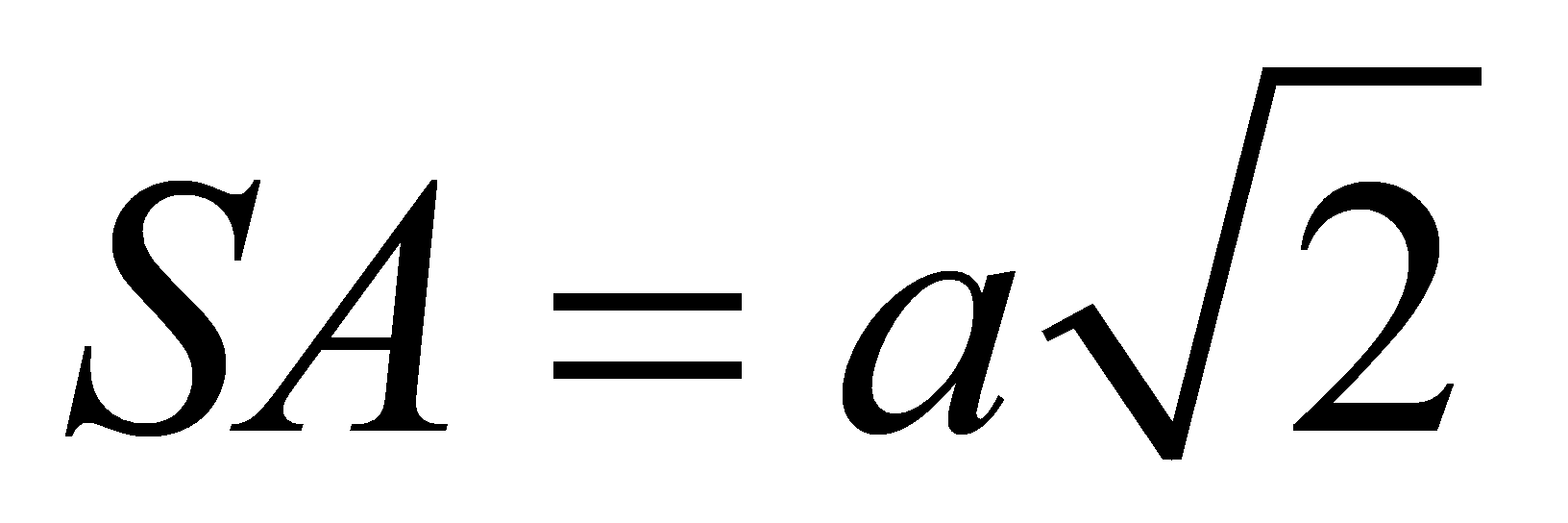 , hình chiếu của điểm
, hình chiếu của điểm  lên mặt phẳng đáy trùng với trung điểm của cạnh huyền
lên mặt phẳng đáy trùng với trung điểm của cạnh huyền 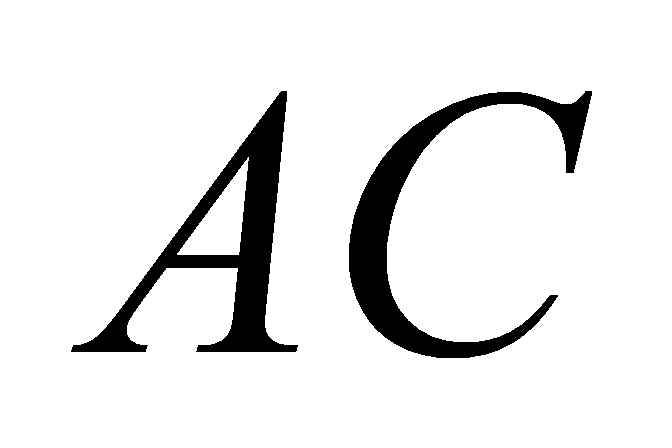 . Tính thể tích khối chóp
. Tính thể tích khối chóp 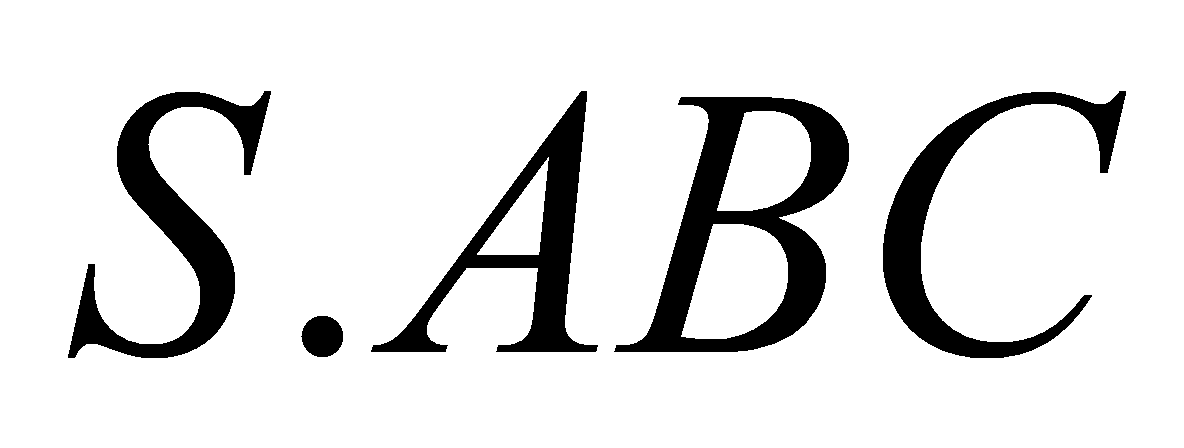 theo
theo  .
.
-
Cho hìnhchóp
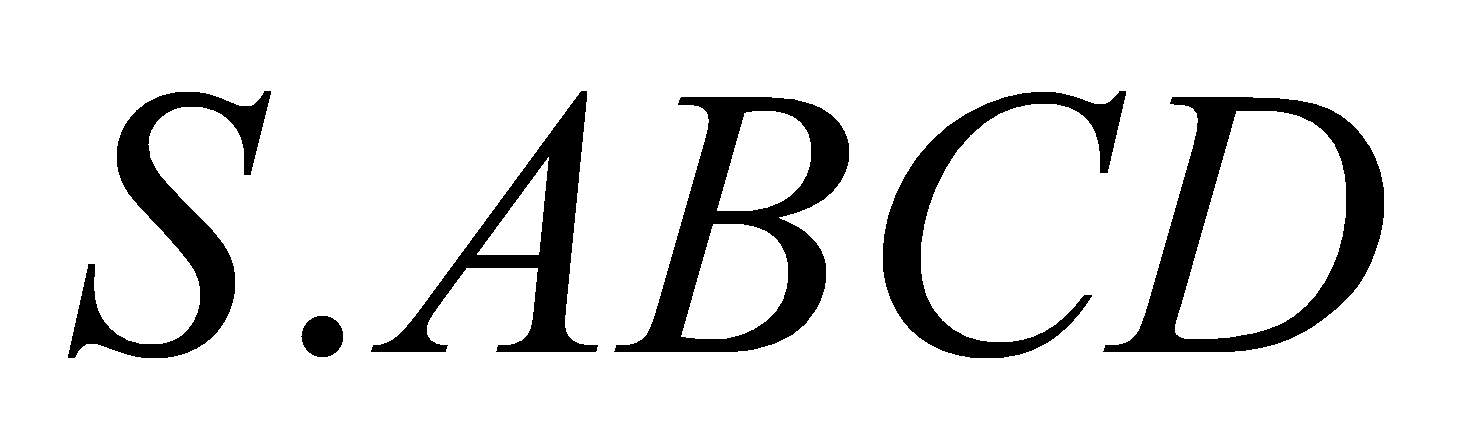 cóđáy
cóđáy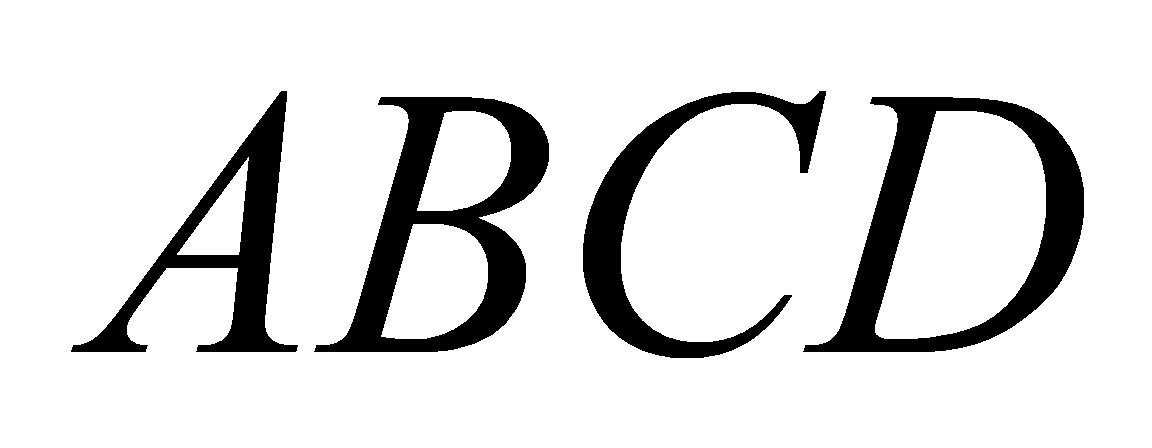 làhìnhchữnhật, tam giác
làhìnhchữnhật, tam giác là tam giácđềucạnh
là tam giácđềucạnh vànằmtrongmặtphẳngvuônggócvớiđáy. Mặtphẳng
vànằmtrongmặtphẳngvuônggócvớiđáy. Mặtphẳng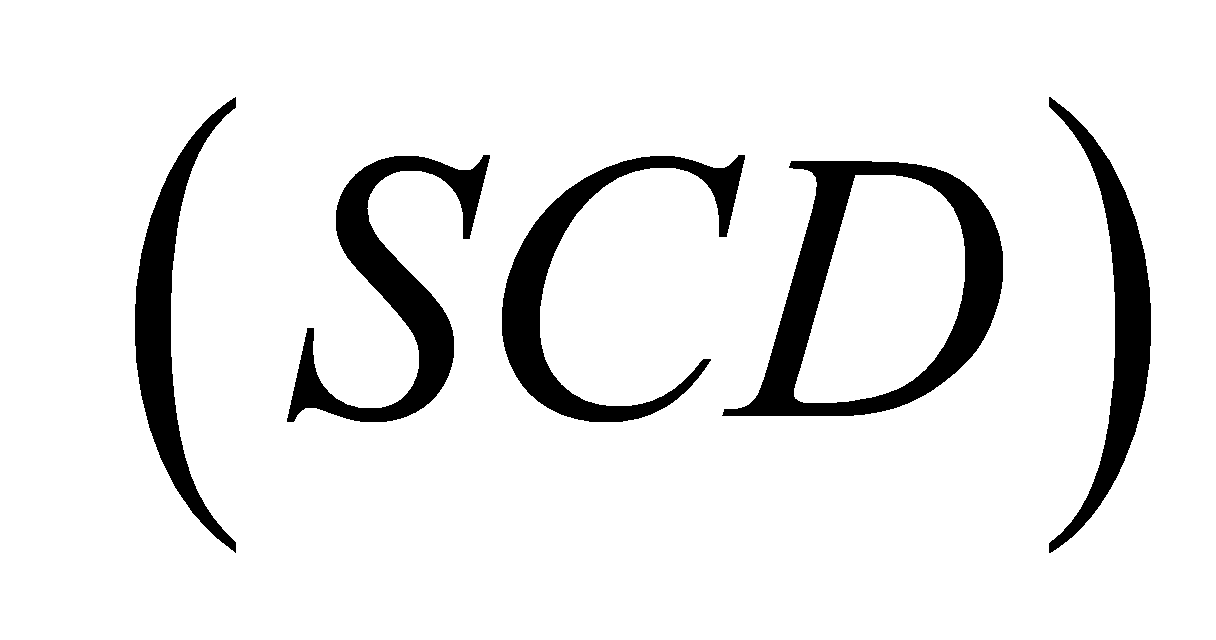 tạovớiđáymộtgóclà
tạovớiđáymộtgóclà . Thểtíchkhốichóp
. Thểtíchkhốichóp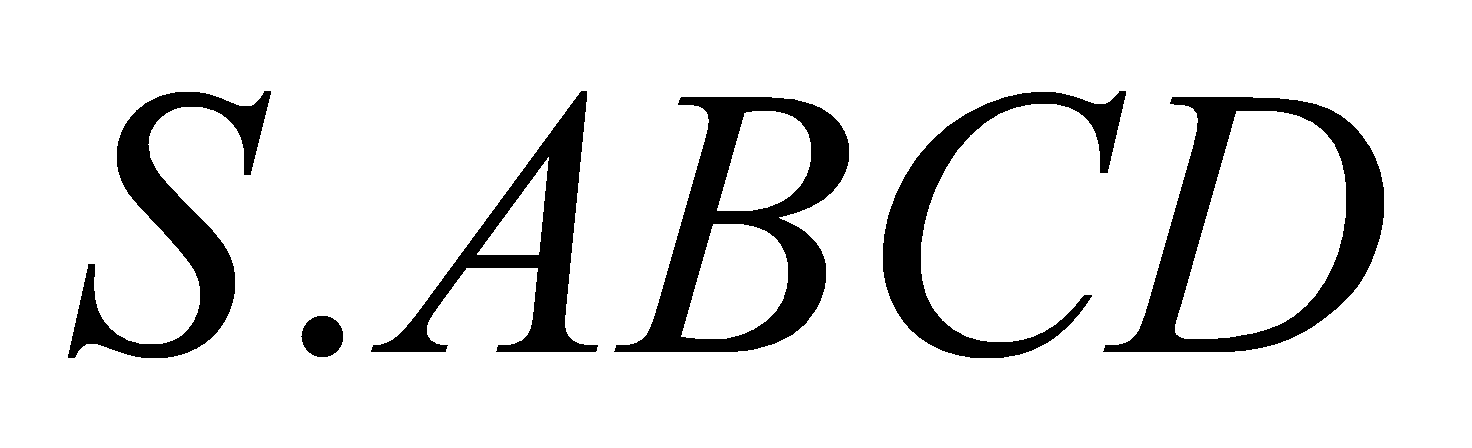 là:
là:
-
Cho hình chóp
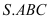 có đáy
có đáy 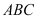 là tam giác đều cạnh
là tam giác đều cạnh 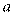 , cạnh bên
, cạnh bên 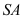 vuông góc với đáy. Tính thể tích khối chóp
vuông góc với đáy. Tính thể tích khối chóp 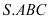 biết
biết 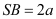
-
Cho khối chóp. S.ABCD có ABCD là hình vuông cạnh 3a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SC và mặt phẳng
 bằng
bằng  .
.
-
Cho hìnhchóp
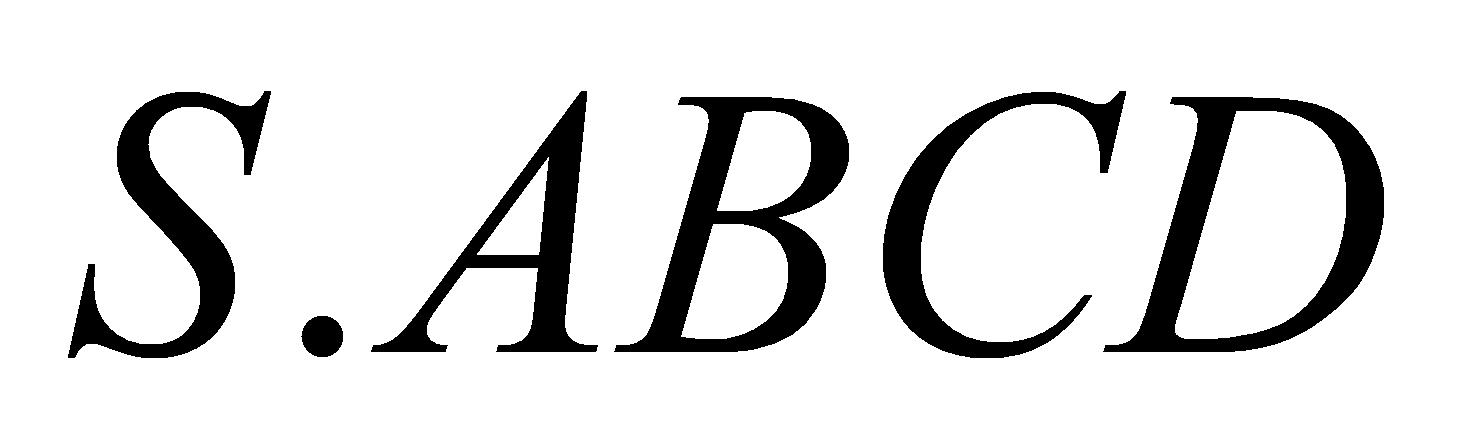 cóđáy
cóđáy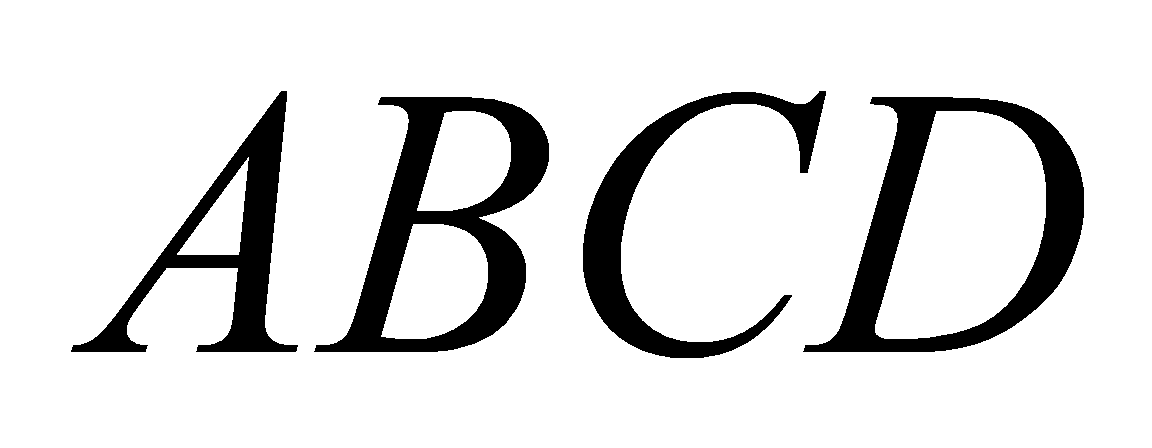 là hìnhvuôngcạnh
là hìnhvuôngcạnh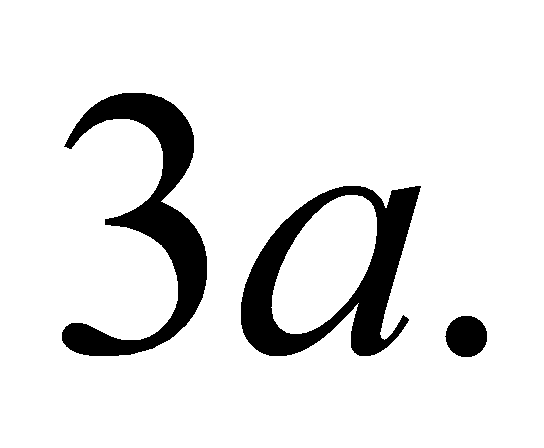 Biếttamgiác
Biếttamgiác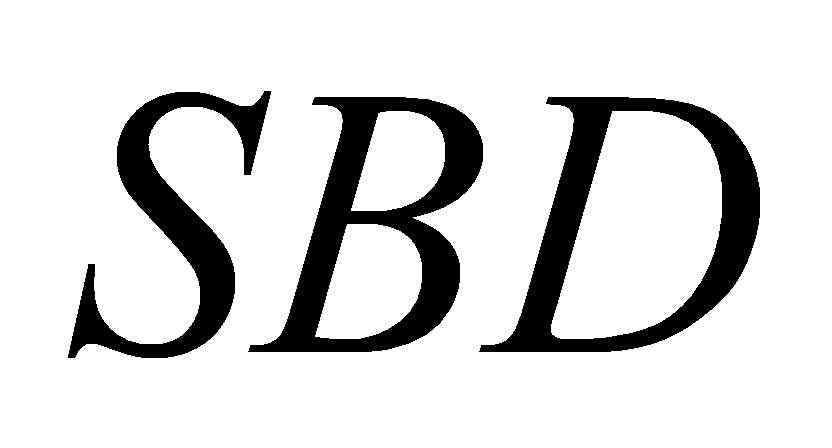 là tamgiácđều, thểtíchkhốichóp
là tamgiácđều, thểtíchkhốichóp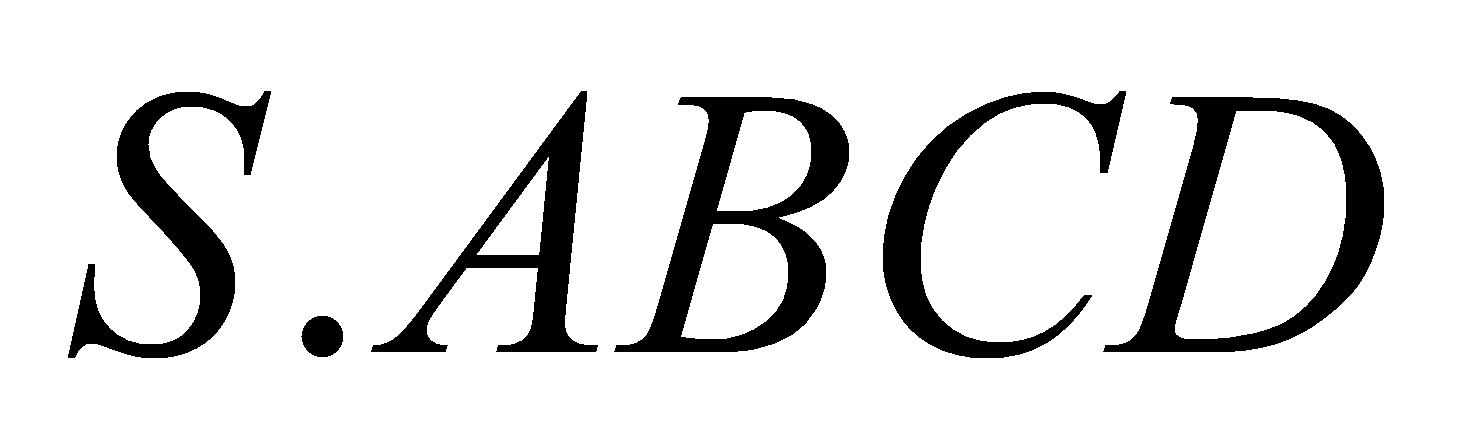 bằng
bằng
-
Cho hình chóp đều
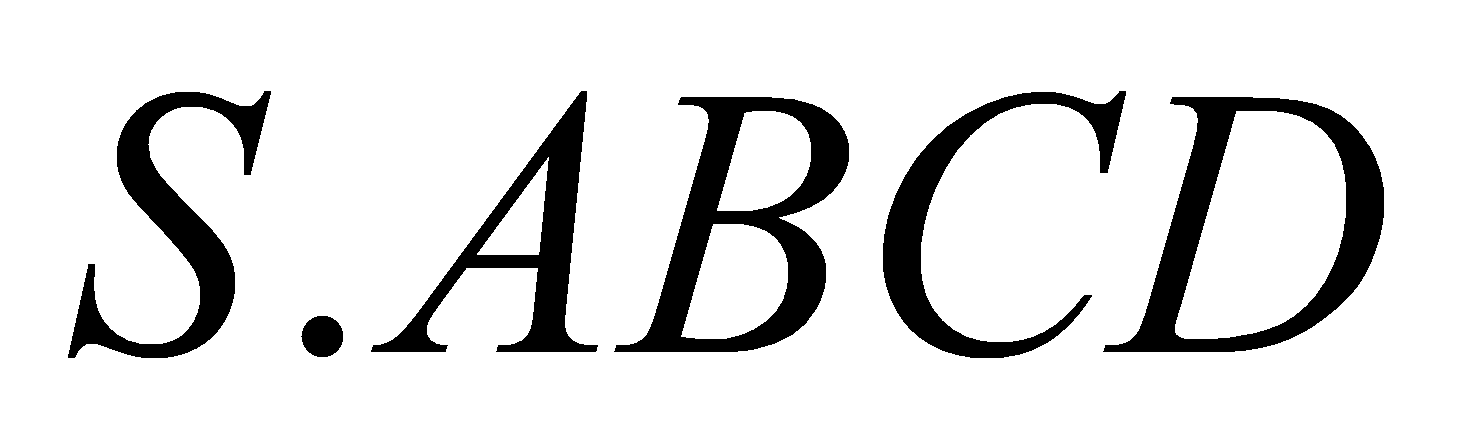 có cạnh đáy bằng
có cạnh đáy bằng  và cạnh bên tạo với đáy một góc
và cạnh bên tạo với đáy một góc  . Tính thể tích của hình chóp đều đó.
. Tính thể tích của hình chóp đều đó.
-
Cho hình chóp đều
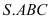 có đáy
có đáy 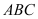 là tam giác đều cạnh
là tam giác đều cạnh 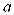 , cạnh bên
, cạnh bên 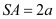 . Tính thể tích
. Tính thể tích 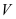 của khối chóp
của khối chóp 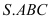
Một số vướng mắc khác hoàn toàn có thể bạn quan tâm.
-
Trong nhiều chủng loại khối đa diện đều sau, tìm khối đa diện có số đỉnh và số mặt phẳng nhau.
-
Cho đa diện (H) có toàn bộ những mặt đều là tứ giác. Khẳng định nào sau này đúng?
-
Trong những mệnh đề sau, mệnh đề nào đúng? Số những cạnh của hình đa diện luôn
-
Trong những mệnh đề sau, mệnh đề nào đúng? Số những đỉnh, hoặc những mặt của bất kỳ hình đa diện luôn
-
Cho đa diện (H) có toàn bộ những mặt đều là tam giác. Khẳng định nào sau này đúng?
-
Cho khối chóp cóđáy là n-giác. Mệnh đề nào sau này đúng?
-
Hình đa diện bên có bao nhiêu mặt?
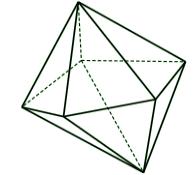
-
Mỗi đỉnh của hình đa diện là đỉnh chung của tối thiểu bao nhiêu mặt?
-
Một hình hộp chữ nhật (không phải hình lập phương) có bao nhiêu mặt phẳng đối xứng?
-
Hìnhnàodướiđâykhôngphảihìnhđadiện?
 Reply
Reply
 6
6
 0
0
 Chia sẻ
Chia sẻ
Chia Sẻ Link Down Cho hình chóp sabc có đáy ABC là tam giác vuông tại đỉnh A cạnh BC 3a miễn phí
Bạn vừa tìm hiểu thêm Post Với Một số hướng dẫn một cách rõ ràng hơn về Review Cho hình chóp sabc có đáy ABC là tam giác vuông tại đỉnh A cạnh BC 3a tiên tiến và phát triển nhất và ShareLink Tải Cho hình chóp sabc có đáy ABC là tam giác vuông tại đỉnh A cạnh BC 3a miễn phí.