Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng xác định Chi tiết
Thủ Thuật Hướng dẫn Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng chừng xác lập 2022
Pro đang tìm kiếm từ khóa Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng chừng xác lập được Cập Nhật vào lúc : 2022-02-12 16:24:04 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y=mx-6/x-m+1 đồng biến trên mỗi khoảng chừng xác lập
6 ngày trước
Điều kiện cần và đủ để hàm số y=(mx+5)/(x+1) đồng biến trên từng khoảng chừng xác lập là
- Leave a comment
Điều kiện cần và đủ để hàm số ( y=fracmx+5x+1 ) đồng biến trên từng khoảng chừng xác lập là
Nội dung chính
- Có bao nhiêu giá trị nguyên của tham số m để hàm số y=mx-6/x-m+1 đồng biến trên mỗi khoảng chừng xác lập
- Điều kiện cần và đủ để hàm số y=(mx+5)/(x+1) đồng biến trên từng khoảng chừng xác lập là
- Các bài toán liên quan
- Tập hợp những giá trị thực của tham số m để hàm số y=x+1+mx−2 đồng biến trên mỗi khoảng chừng xác lập của nó là
- Bài tập trắc nghiệm 15 phút Tìm Đk của tham số để hàm số đơn điệu trên tập xác lập. – Toán Học 12 – Đề số 12
- Tóm tắt lý thuyết tính đồng biến nghịch biến
- 1. Định nghĩa đồng biến, nghịch biến
- 2. Định lí
- 3. Định lí mở rộng
- 4. Qui tắc xét tính đơn điệu của hàm số
Khẳng định nào sau này là đúng về hàm số
.
Tìm tất cảgiátrịcủa sốthực
đểhàm số
đồng biến trên
Tìm toàn bộ những giá trị m để hàm số y=13×3−mx22+2x+2022 đồng biến trên ℝ .
Cóbao nhiêu giátrịnguyên của tham số
đểhàm số
nghịch biến trên khoảng chừng
?
Tìm
để hàm số
đồng biến trên từng khoảng chừng xác lập của chúng.
Tập hợp những giá trị thực của tham số m để hàm số y=x+1+mx−2 đồng biến trên mỗi khoảng chừng xác lập của nó là
Hàm số y=13×3−(m+3)x−2022 luôn đồng biến trên ℝ thì:
Có bao nhiêu giá trị nguyên của tham số m trên −1;5 để hàm số y=13×3-x2+mx+1 đồng biến trên khoảng chừng −∞;+∞ ?
Có bao nhiêu giá trị nguyên của m để hàm số y=3x+msinx+cosx+m đồng biến trên ℝ ?
Hỏi có bao nhiêu giá trị nguyên m để hàm số y=mét vuông−1×3+m−1×2−x+4 nghịch biến trên khoảng chừng −∞;+∞ ?
Một cuộn dây có N = 600 vòng, diện tích s quy hoạnh mỗi vòng S = 40 cm2. Hai đầu cuộn dây được nối với một điện kế. Cuộn dây được đặt trong một từ trường đều phải có đường cảm ứng từ tuy nhiên tuy nhiên với trục cuộn dây và cường độ của
biến hóa đều từ giá trị ban đầu B0 = 0 đến B = 4.10-2 T trong mức chừng thời hạn Δt = 0,2 s.
Độ biến thiên của từ thông là
* Cho một dòng điện có cường độ I = 5 (A) chạy trong một dây dẫn thẳng dài vô hạn đặt trong không khí.
Cảm ứng từ B1 tại điểm M1 cách dây dẫn một khoảng chừng r1 = 5 (cm) là
Một cuộn dây có N = 600 vòng, diện tích s quy hoạnh mỗi vòng S = 40 cm2. Hai đầu cuộn dây được nối với một điện kế. Cuộn dây được đặt trong một từ trường đều phải có đường cảm ứng từ tuy nhiên tuy nhiên với trục cuộn dây và cường độ của
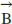 biến hóa đều từ giá trị ban đầu B0 = 0 đến B = 4.10-2 T trong mức chừng thời hạn Δt = 0,2 s.
biến hóa đều từ giá trị ban đầu B0 = 0 đến B = 4.10-2 T trong mức chừng thời hạn Δt = 0,2 s.Suất điện động cảm ứng xuất hiện trong cuộn dây là
* Cho một dòng điện có cường độ I = 5 (A) chạy trong một dây dẫn thẳng dài vô hạn đặt trong không khí.
Tại điểm M2, vectơ cảm ứng từ có độ lớn B2 = 4.10-6 (T). Khoảng cách r2 từ M2 đến dây dẫn là
Một ống dây gồm N = 800 vòng dây, có chiều dài l = 40 cm, diện tích s quy hoạnh mỗi vòng S = 20 cm2, có dòng điện I = 6 A trải qua:
Từ thông Φ1 trải qua mỗi vòng dây là
Một ống dây gồm N = 800 vòng dây, có chiều dài l = 40 cm, diện tích s quy hoạnh mỗi vòng S = 20 cm2, có dòng điện I = 6 A trải qua.
Suất điện động tự cảm xuất hiện trong ống dây khi ngắt dòng điện trong thời hạn Δt = 1 s, giả thử B giảm đều theo thời hạn là
Một ống dây gồm N = 800 vòng dây, có chiều dài l = 40 cm, diện tích s quy hoạnh mỗi vòng S = 20 cm2, có dòng điện I = 6 A trải qua.
Độ tự cảm của ống dây là
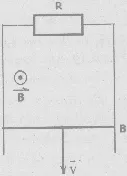
Cho hai thanh sắt kẽm kim loại tuy nhiên tuy nhiên,
thẳng đứng, điện trở không đáng kể, một đầu nối
với điện trở R = 1,5Ω. Một thanh dây dẫn AB, có
chiều dài l = 15 cm, khối lượng m = 2,5 g, điện trở
R = 1,5Ω trượt không ma sát xuống dưới với vận
tốc v và luôn luôn vuông gốc với hai thanh sắt kẽm kim loại.
Toàn bộ khối mạng lưới hệ thống được đặt trong từ trường
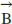 có
cóphương vuông góc với mặt phẳng hai thanh kim
loại, chiều như hình vẽ, có cảm ứng từ B = 0,5 T.
Cho g = 9,8 m/s2.
Chiều dòng điện qua AB và biểu thức của cường độ dòng điện là
Cho hai dây dẫn thẳng tuy nhiên tuy nhiên dài vô hạn cách nhau một khoáng 2a = 20 (cm)
đặt trong không khí, trong số đó có hai dòng điện chạy ngược chiều nhau, cường độ lần lượt là I1 = I2 = I = 10 (A). Một mặt phẳng P trải qua một điểm M cắt hai dây tại hai điểm A và B. M nằm trên đường trung trực của AB và cách AB một khoảng chừng 2a. Vectơ cảm ứng từ tổng hợp tại M là
Cho hai thanh sắt kẽm kim loại tuy nhiên tuy nhiên,
thẳng đứng, điện trở không đáng kể, một đầu nối
với điện trở R = 1,5Ω. Một thanh dây dẫn AB, có
chiều dài l = 15 cm, khối lượng m = 2,5 g, điện trở
R = 1,5Ω trượt không ma sát xuống dưới với vận
tốc v và luôn luôn vuông gốc với hai thanh sắt kẽm kim loại.
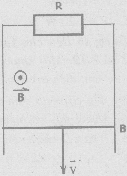
Toàn bộ khối mạng lưới hệ thống được đặt trong từ trường
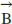 có
cóphương vuông góc với mặt phẳng hai thanh kim
loại, chiều như hình vẽ, có cảm ứng từ B = 0,5 T.
Cho g = 9,8 m/s2 và dòng điện qua AB có chiều từ B sang A, I =
Vận tốc số lượng giới hạn v0 của thanh AB là
A. ( m>-5 )
B. ( mge -5 )
C. ( mge 5 )
D. ( m>5 )
Hướng dẫn giải:
Đáp án D.
Yêu cầu bài toán tương tự: ( y’=fracm-5(x+1)^2>0,forall xne -1 )
( Leftrightarrow m-5>0Leftrightarrow m>5 )
Các bài toán liên quan
Cho hàm số y=asinx+bcosx+x với a, b là những tham số thực. Điều kiện của a, b để hàm số đồng biến trên R
Xem lời giải!
Cho hai hàm số f(x)=x+msinx và g(x)=(m−3)x−(2m+1)cosx. Tất cả những giá trị của m làm cho hàm số f(x) đồng biến trên R và g(x) nghịch biến trên R
Xem lời giải!
Cho hàm số y=(x2+1−−−−−√−x)3−m(2×2−2xx2+1−−−−−√+1)−m−6×2+1√+x−1. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số nghịch biến trên R
Xem lời giải!
Cho hàm số y=(m−1)x−1√+2x−1√+m. Tìm tập toàn bộ những giá trị của tham số m để hàm số đồng biến trên khoảng chừng (17;37)
Xem lời giải!
Tìm toàn bộ những giá trị thực của tham số m để hàm số y=(m−sinx)/cos^2x nghịch biến trên (0;π/6)
Xem lời giải!
Tìm toàn bộ những giá trị thực của tham số m sao cho hàm số y=(tanx−2)/(tanx−m) đồng biến trên khoảng chừng (0;π/4)
Xem lời giải!
Tất cả những giá trị thực của tham số m để hàm số y=(sinx+m)/(sinx−m) nghịch biến trên khoảng chừng (π2;π)
Xem lời giải!
Tập hợp những giá trị thực của tham số m để hàm số y=x+1+mx−2 đồng biến trên mỗi khoảng chừng xác lập của nó là
A.0; 1 .
B.−∞; 0 .
C.0; +∞1 .
D.−∞; 0 .
Đáp án và lời giải
Đáp án:B
Lời giải:Lời giải
Chọn B
• Tập xác lập: D=ℝ2 .
Hàm số đã cho đồng biến trên mỗi khoảng chừng xác lập của nó khi và chỉ khi:
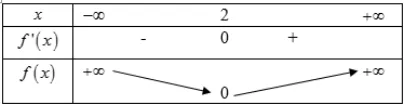
y’≥0, ∀x∈D ⇔1−mx−22≥0, ∀x∈D ⇔m≤x−22, ∀x∈D
Xét hàm số fx=x−22 ta có: f’x=2x−4⇒f’x=0⇔x=2
Bảng biến thiên:
Vậy, để hàm số đã cho đồng biến trên mỗi khoảng chừng xác lập của nó thì m≤0 .
Vậy đáp án đúng là B.
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 15 phút Tìm Đk của tham số để hàm số đơn điệu trên tập xác lập. – Toán Học 12 – Đề số 12
Làm bài
Chia sẻ
Một số vướng mắc khác cùng bài thi.
Một số vướng mắc khác hoàn toàn có thể bạn quan tâm.
Tóm tắt lý thuyết tính đồng biến nghịch biến
1. Định nghĩa đồng biến, nghịch biến
Cho hàm số y = f(x) xác lập trên K , trong số đó K là một khoảng chừng, đoạn hoặc nữa khoảng chừng.
a) Hàm số y = f(x) đồng biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).
b) Hàm số y = f(x) nghịch biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) > f(x₂).
2. Định lí
Cho hàm số y = f(x) có đạo hàm trên K .
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K .
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K .
c) Nếu f’(x) = 0 với mọi x thuộc K thì hàm số f(x) không đổi trên K .
Chú ý: Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) > 0 trên khoảng chừng (a;b) thì hàm số f đồng biến trên đoạn [a;b]. Nếu hàm số f liên tục trên đoạn [a;b] và có đạo hàm f’(x) < 0 trên khoảng chừng (a;b) thì hàm số f nghịch biến trên đoạn [a;b].
3. Định lí mở rộng
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) ≥ 0 với mọi x thuộc K và f’(x) = 0 xẩy ra tại một số trong những hữu hạn điểm của K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) ≤ 0 với mọi x thuộc K và f’(x) = 0 xẩy ra tại một số trong những hữu hạn điểm của K thì hàm số f(x) nghịch biến trên K.
4. Qui tắc xét tính đơn điệu của hàm số
Bước 1: Tìm tập xác lập.
Bước 2: Tính đạo hàm f’(x). Tìm những điểm xᵢ (i = 1, 2, …,n) mà tại đó đạo hàm bằng 0 hoặc không xác lập.
Bước 3: Sắp xếp những điểm xᵢ theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Nêu kết luận về những khoảng chừng đồng biến, nghịch biến của hàm số.
Reply
6
0
Chia sẻ
Share Link Download Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng chừng xác lập miễn phí
Bạn vừa Read Post Với Một số hướng dẫn một cách rõ ràng hơn về Clip Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng chừng xác lập tiên tiến và phát triển nhất và Chia SẻLink Tải Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng chừng xác lập miễn phí.

Hỏi đáp vướng mắc về Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng chừng xác lập
Nếu sau khi đọc nội dung bài viết Có bao nhiêu giá trị nguyên của tham số m để hàm số y mx 6 x m 1 đồng biến trên mỗi khoảng chừng xác lập vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Có #bao #nhiêu #giá #trị #nguyên #của #tham #số #để #hàm #số #đồng #biến #trên #mỗi #khoảng chừng #xác #định