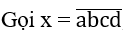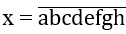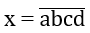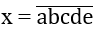Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4 Chi tiết
Thủ Thuật Hướng dẫn Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4 Chi Tiết
Bạn đang tìm kiếm từ khóa Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4 được Cập Nhật vào lúc : 2022-12-07 02:43:05 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Đếm số phương án liên quan đến số tự nhiên
Trang trước
Trang sau
Quảng cáo
Ta sử dụng phương pháp chung và một số trong những lưu ý sau:
Khi lập một số trong những tự nhiên 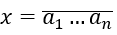
* ai 0,1,2,,9 và a1 0.
* x là số chẵn an là số chẵn.
* x là số lẻ an là số lẻ.
* x chia hết cho 3 a1+a2++an chia hết cho 3.
* x chia hết cho 4 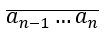
* x chia hết cho 5 an=0 hoặc an=5.
* x chia hết cho 6 x là số chẵn và chia hết cho 3.
* x chia hết cho 8 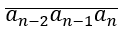
* x chia hết cho 9 a1+a2++an chia hết cho 9.
* x chia hết cho 11 tổng những chữ số ở hàng lẻ trừ đi tổng những chữ số ở hàng chẵn là một số trong những chia hết cho 11.
* x chia hết cho 25 hai chữ số tận cùng là 00, 25, 50, 75.
Bài 1: Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một rất khác nhau được lập từ những số 0,1,2,4,5,6,8.
Đáp án và hướng dẫn giải
a,b,c,d 0,1,2,4,5,6,8, a 0.
Vì x là số chẵn nên d 0,2,4,6,8.
TH1: d = 0 có một cách chọn d.
Vì a 0 nên ta có 6 cách chọn a 1,2,4,5,6,8.
Với mỗi cách chọn a, d ta có 5 cách chọn b 1,2,4,5,6,8a.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c 1,2,4,5,6,8a,b.
Suy ra trong trường hợp này còn có một.6.5.4 = 120 số.
TH2: d 0, d chẵn nên d 2,4,6,8. Vậy có 4 cách chọn d
Với mỗi cách chọn d, do a 0 nên ta có 5 cách chọn a 1,2,4,5,6,8d.
Với mỗi cách chọn a,d ta có 5 cách chọn b 0,1,2,4,5,6,8a,d.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c 0,1,2,4,5,6,8a,d,b.
Suy ra trong trường hợp này còn có 4.5.5.4= 400 số.
Vậy có toàn bộ 120 + 400 = 520 số cần lập.
Quảng cáo
Bài 2: Cho tập A = 0,1,2,3,4,5,6.Từ tập A ta hoàn toàn có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một rất khác nhau.
Đáp án và hướng dẫn giải
a,b,c,d 0,1,2,3,4,5,6, a 0.
Vì a 0 nên a có 6 cách chọn a 1,2,3,4,5,6.
Với mỗi cách chọn a ta có 6 cách chọn b 0,1,2,3,4,5,6a.
Với mỗi cách chọn a,b ta có 5 cách chọn c 0,1,2,3,4,5,6a,b.
Với mỗi cách chọn a,b, c ta có 4 cách chọn d 0,1,2,3,4,5,6a,b,c.
Vậy có 6.6.5.4 = 720 số cần lập.
Bài 3: Cho tập A = 1,2,3,4,5,6,7,8.
Từ tập A hoàn toàn có thể lập được bao nhiêu số gồm 8 chữ số đôi một rất khác nhau sao những số này lẻ không chia hết cho 5.
Đáp án và hướng dẫn giải
a,b,c,d,e,f,g,h 1,2,3,4,5,6,7,8 là số cần tìm.
Vì x lẻ và không chia hết cho 5 nên h 1,3,7 nên h có 3 cách chọn
Số những chọn những chữ số còn sót lại là: 7.6.5.4.3.2.1
Vậy 15120 số thỏa yêu cầu bài toán.
Bài 1: Cho tập A = 0,1,2,3,4,5,6. Từ tập A ta hoàn toàn có thể lập được bao nhiêu số tự nhiên lẻ gồm 4 chữ số đôi một rất khác nhau
Lời giải:
a,b,c,d 0,1,2,3,4,5,6,a 0
Vì x là số lẻ nên d 1,3,5 vậy d có 3 cách chọn.
Vì a 0 và với mỗi cách chọn d ta có 5 cách chọn a 1,2,3,4,5,6d.
Với mỗi cách chọn a, d ta có 5 cách chọn b 0,1,2,3,4,5,6a,d.
Với mỗi cách chọn a, b, d ta có 4 cách chọn c 0,1,2,3,4,5,6a,b,d.
Suy ra trong trường hợp này còn có 3.5.5.4 = 300 số.
Quảng cáo
Bài 2: Cho tập A = 0,1,2,3,4,5,6. Từ tập A hoàn toàn có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số và chia hết cho 5.
Lời giải:
a,b,c,d,e 0,1,2,3,4,5,6,a 0 là số cần lập, e 0,5.
TH1: e = 0 suy ra có một cách chọn, số cách chọn a,b,c,d là 6.5.4.3
Trường hợp này còn có 360 số
TH2: e = 5 suy ra e có một cách chọn, số cách chọn a,b,c,d là 5.5.4.3 = 300.
Trường hợp này còn có 300 số
Vậy có 660 số thỏa yêu cầu bài toán.
Bài 3: Cho tập hợp số A = 0,1,2,3,4,5,6. Hỏi hoàn toàn có thể xây dựng bao nhiêu số có 4 chữ số rất khác nhau và chia hết cho 3.
Lời giải:
Ta có một số chia hết cho 3 khi và chỉ khi tổng các chữ số chia hết cho 3. Trong tập. A có các tập. con các chữ số chia hết cho 3 là 0,1,2,3, 0,1,2,6,0,2,3,4, 0,3,4,5, 1,2,4,5, 1,2,3,6, 1,3,5,6.
Vậy số các số cần lập. là: 4(4! 3!) + 3.4! = 144 số.
Bài 4: Có bao nhiêu số những số tự nhiên gồm chữ số chia hết cho 10?
Lời giải:
a,b,c,d,e là những chữ số, a 0.
Vì x chia hết cho 10 nên e = 0, vậy e có một cách chọn.
Chọn a có 9 cách chọn a 1,2,3,4,5,6,7,8,9.
Chọn b có 10 cách chọn b 0,1,2,3,4,5,6,7,8,9.
Chọn c có 10 cách chọn c 0,1,2,3,4,5,6,7,8,9
Chọn d có 10 cách chọn d 0,1,2,3,4,5,6,7,8,9
Vậy số những số cần lập là một trong.9.10.10.10 = 9000 số.
Bài 5: Cho tập A = 1,2,3,4,5,6,7,8. Từ tập A hoàn toàn có thể lập được bao nhiêu số gồm 8 chữ số đôi một rất khác nhau sao cho chữ số đầu chẵn và chữ số đứng cuối lẻ.
Lời giải:
Với a, b, c, d, e, f, g, h 1, 2, 3, 4, 5, 6, 7, 8 là số cần tìm.
Vì chữ số đứng đầu chẵn nên a có 4 cách chọn, chữ số đứng cuối lẻ nên h có 4 cách chọn.
Với mỗi cách chọn a và h thì sẽ có được 6 cách chọn b; 5 cách chọn c; 4 cách chọn d, 3 cách chọn e; 2 cách chọn f và 1 cách chọn g.
Vậy có 4.4.6.5.4.3.2.1 = 11 520 số thỏa yêu cầu bài toán.
Xem thêm những dạng bài tập Toán lớp 11 có trong đề thi THPT Quốc gia khác:
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Chia Sẻ Link Tải Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4 miễn phí
Bạn vừa tìm hiểu thêm nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Clip Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4 tiên tiến và phát triển nhất và Share Link Cập nhật Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4 miễn phí.

Hỏi đáp vướng mắc về Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4
Nếu sau khi đọc nội dung bài viết Có bao nhiêu số tự nhiên có hai chữ số chia hết cho 4 vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Có #bao #nhiêu #số #tự #nhiên #có #hai #chữ #số #chia #hết #cho